��Ŀ����
7����ѧ��ʦ����������һ�����}����������¶�Ϊ��ǣ���tan��=$\frac{1}{3}$��tan��=$\frac{1}{2}$�����+�µĶ�����
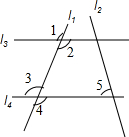
�ס�����λͬѧ����������������ͼ��������⣮���Ƿֱ������ͼ1��ͼ2��
��1������ֱ�����ͼ1��ͼ2�����+�µĶ�������˵�����ɣ�
��2����ο�����˼������ķ�����ѡ��һ�ַ�������������⣺
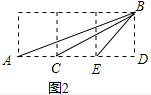
��������¶�Ϊ��ǣ���tan��=5��tan��=$\frac{2}{3}$ʱ����ͼ3�������������У���������������Ǧ���������MON��ʹ�á�MON=��-�£������-�µĶ�������˵�����ɣ�
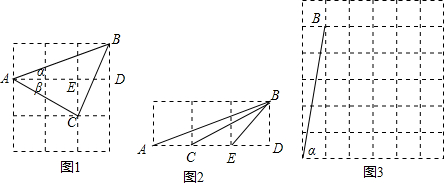
���� ��1��������ͼ1�У�ֻҪ֤����AMC�ա�CNB������֤����ACB�ǵ���ֱ�������Σ�
����ͼ2�У�ֻҪ֤����CEB�ס�BEA������֤����BED=��+��=45�㣮
��2����ͼ3�У���MOE=������NOH=�£���MON=��-�£�ֻҪ֤����MFN�ա�NHO���ɽ�����⣮
��� �⣺��1������ͼ1�У�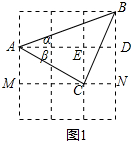
�ڡ�AMC�͡�CNB�У�
$\left\{\begin{array}{l}{AM=CN}\\{��AMC=��CNB=90��}\\{MC=BN}\end{array}\right.$��
���AMC�ա�CNB��
��AC=BC����ACM=��CBN��
�ߡ�BCN+��CBN=90�㣬
���ACM+��BCN=90�㣬
���ACB=90�㣬
���CAB=��CBA=45�㣬
���+��=45�㣮
�� ��ͼ2�У��������α߳�Ϊ1����CE=1��AE=2��BE=$\sqrt{2}$��
��ͼ2�У��������α߳�Ϊ1����CE=1��AE=2��BE=$\sqrt{2}$��
��$\frac{EC}{BE}$=$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$��$\frac{BE}{AE}$=$\frac{\sqrt{2}}{2}$��
��$\frac{EC}{BE}$=$\frac{BE}{AE}$��
�ߡ�CEB=��AEB
���CEB�ס�BEA��
���CAB=��CBE=����
�ߡ�BED=��ECB+��CBE=��+�£�
��DE=DB����D=90�㣬
��BED=45�㣬
���+��=45�㣮
��2����ͼ3�У���MOE=������NOH=�£���MON=��-�£�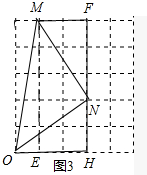
�ڡ�MFN�͡�NHO�У�
$\left\{\begin{array}{l}{MF=NH}\\{��MFN=��NHO}\\{FN=OH}\end{array}\right.$��
���MFN�ա�NHO��
��MN=NO����MNF=��NOH��
�ߡ�NOH+��ONH=90�㣬
���ONH+��MNF=90�㣬
���MNO=90�㣬
���NOM=��NMO=45�㣬
���-��=45�㣮
���� ���⿼������ͼ-Ӧ�������ͼ��ȫ�������ε��ж������ʡ����������ε��ж������ʣ�����ֱ�������ε��ж������ʣ����ɶ�����֪ʶ�����ݺ���ֵ����ֱ���������ǽ���Ĺؼ��������п�������Ŀ��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | 5-x=4��x-3�� | B�� | 5+x=4��x-3�� | C�� | 5��3-x��+x��x-3��=4 | D�� | 5-x=4 |
| ��� | Aվ | Bվ | Cվ | �յ� | |
| �ϡ��³˿����� | 18 | 15 | 12 | 7 | 0 |
| 0 | -3 | -4 | -10 | -35 |
��2����������ʻ������վ֮�䳵�ϵij˿���ࣿ����ʽ˵�����ɣ�
��3�����˹���������һƱ�ƣ���ÿλ�ϳ��˿�������վ�³�����Ʊ����2Ԫ���ʸó���γ������������Ǯ������ʽ���㣮
 ��ͼ��
��ͼ��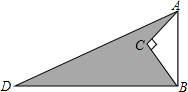 ��ͼ����Rt��ABD�У�AD=13��BD=12�����ڡ�ABD����һ��C������AC=3��BC=4����C=90�㣬����Ӱ���ֵ����Ϊ24��
��ͼ����Rt��ABD�У�AD=13��BD=12�����ڡ�ABD����һ��C������AC=3��BC=4����C=90�㣬����Ӱ���ֵ����Ϊ24��