题目内容
6.若方程x2-x+p=0的两根之比为3,则p=$\frac{3}{16}$.分析 先根据判别式的意义确定p的取值范围,设方程的两根为3t,t,先根据两根之和得到t的数值,然后利用两根之积计算p的值.
解答 解:根据题意得△=12-4p>0,解得p<$\frac{1}{4}$,
设方程的两根为3t,t,则3t+t=1,3t•t=p,
解得t=$\frac{1}{4}$,
所以p=$\frac{3}{16}$.
故答案为:$\frac{3}{16}$.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个为x1,x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.

练习册系列答案
相关题目
16.分式$\frac{{a}^{2}+a}{{a}^{2}+2a+1}$化简的结果是( )
| A. | $\frac{a}{a-1}$ | B. | $\frac{a+1}{a-1}$ | C. | $\frac{a}{a+1}$ | D. | a |
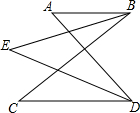 已知,如图,AB∥CD,BE平分∠ABC,DE平分∠ADC,求证:∠E=$\frac{1}{2}$(∠A+∠C)
已知,如图,AB∥CD,BE平分∠ABC,DE平分∠ADC,求证:∠E=$\frac{1}{2}$(∠A+∠C)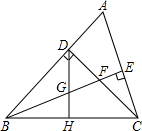 已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH与BE相交于点G.
已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH与BE相交于点G.