题目内容
14. 如图所示,AD⊥BC于点D,EG⊥BC于点G,若∠E=∠1,则∠2=∠3吗?
如图所示,AD⊥BC于点D,EG⊥BC于点G,若∠E=∠1,则∠2=∠3吗?下面是推理过程,请你填空或填写理由.
证明:∵AD⊥BC于点D,EG⊥BC于点G(已知),
∴∠ADC=∠EGC=90°垂直的定义,
∴AD∥EG(同位角相等,两直线平行),
∴∠1=∠2(两直线平行,同位角相等),
∵∠E=∠1(已知)
∴∠E=∠2(等量代换)
∵AD∥EG,
∴∠E=∠3(两直线平行,同位角相等).
∴∠2=∠3(等量代换)
分析 根据垂直的定义得到∠ADC=∠EGC=90°,根据平行线的判定得到AD∥EG,由平行线的性质得到∠1=∠2,等量代换得到∠E=∠2,由平行线的性质得到∠E=∠3,等量代换即可得到结论.
解答 证明:∵AD⊥BC于点D,EG⊥BC于点G(已知),
∴∠ADC=∠EGC=90°(垂直的定义),
∴AD∥EG(同位角相等,两直线平行),
∴∠1=∠2(两直线平行,内错角相等),
∵∠E=∠1(已知)
∴∠E=∠2(等量代换)
∵AD∥EG,
∴∠E=∠3(两直线平行,同位角相等).
∴∠2=∠3(等量代换),
故答案为:垂直的定义,同位角相等,两直线平行,两直线平行,同位角相等,∠E,∠2,∠3.
点评 本题考查了平行线的性质,垂直的定义,熟练掌握平行线的性质是解题的关键.

练习册系列答案
相关题目
5.化简$\frac{x}{x-1}-\frac{1}{1-x}$的结果为( )
| A. | -1 | B. | 1 | C. | $\frac{x+1}{x-1}$ | D. | $\frac{x+1}{1-x}$ |
2.表为甲班55人某次数学小考成绩的统计结果,关于甲班男、女生此次小考成绩的统计量,下列叙述何者正确?( )
| 成绩(分) | 50 | 70 | 90 |
| 男生(人) | 10 | 10 | 10 |
| 女生(人) | 5 | 15 | 5 |
| 合计(人) | 15 | 25 | 15 |
| A. | 男生成绩的四分位距大于女生成绩的四分位距 | |
| B. | 男生成绩的四分位距小于女生成绩的四分位距 | |
| C. | 男生成绩的平均数大于女生成绩的平均数 | |
| D. | 男生成绩的平均数小于女生成绩的平均数 |
4.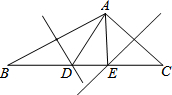 如图,△ABC中,∠BAC>90°,其中AB、AC的垂直平分线交BC于点D、E,△ADE的周长为16,则BC的长( )
如图,△ABC中,∠BAC>90°,其中AB、AC的垂直平分线交BC于点D、E,△ADE的周长为16,则BC的长( )
 如图,△ABC中,∠BAC>90°,其中AB、AC的垂直平分线交BC于点D、E,△ADE的周长为16,则BC的长( )
如图,△ABC中,∠BAC>90°,其中AB、AC的垂直平分线交BC于点D、E,△ADE的周长为16,则BC的长( )| A. | 16 | B. | 18 | C. | 24 | D. | 32 |
 如图,在△ABC中,∠B=42°,∠C=78°,AD平分∠BAC.
如图,在△ABC中,∠B=42°,∠C=78°,AD平分∠BAC.