题目内容
已知∠B为△ABC的内角,且sinB与cosB恰好为方程mx2-mx+p-4=0的两根,以AB为直径的⊙O交AC于D ,取BC的中点E,经过A、B、E的⊙O′交直线DE于F,如图,连接AF.
,取BC的中点E,经过A、B、E的⊙O′交直线DE于F,如图,连接AF.
(1)求证:EF为⊙O的切线;
(2)求证:AD2=AF•AB;
(3)若⊙O的半径R=p,且AD:CD=2:3,求弦EF的长及tan∠ABF.
(1)证明:∵sinB与cosB是方程mx2-mx+p-4=0的两根,
∴sinB+cosB=1,
∴sin2B+2sinBcosB+cos2B=1,
又sin2B+cos2B=1,
故:sinBcosB=0,
由于∠B为三角形内角,
∴∠B≠0,
∴sinB≠0,
从而cosB=0,则∠B=90°;
连接OD、OE.如图
∵O、E分别为AB、BC的中点,
∴OE为△ABC的中位线,
则OE∥AC,
∴∠CAB=∠EOB,∠ADO=∠DOE,
由于:OA=OD,
∴∠OAD=∠ADO,
∴∠BOE=DOE,
在△BOE与△DOE中: ,
,
∴△BOE≌△DOE,
∴∠OBE=∠ODE=90°,
∴OD⊥DE,
∴EF为⊙O的切线;
(2)解:连接BD.
∵四边形A、B、E、F四点共圆,且∠ABE=90°,
∴∠ABE=∠AFE=90°,
由EF为⊙O的切线,
∴∠ABD=∠ADF,
又∵AB为⊙O的直径,
∴∠ADB=90°=∠AFE,
∴△AFD∽△ADB,从而有AF:AD=AD:AB,
即有AD2=AF•AB;
(3)解:由于∠B=90°,
∴sinB=1,cosB=0,
∴sinB•cosB= =0,
=0,
∵m≠0,p-4=0,
∴p=4,即R=4,
设AD=2x,则CD=3x,AC=5x,
在⊙O中,由切割线定理得: CD•CA=CB2,而CB2=AC2-AB2
CD•CA=CB2,而CB2=AC2-AB2
∴3x•5x=(5x)2-82
∴15x2=25x2-64,
解得:x=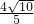 ,
,
∴CB=4 ,
,
∴DE= CB=2
CB=2 ,
,
且AD=2x= ,又有AD2=AF•AB,
,又有AD2=AF•AB,
∴AF=( )2÷8=
)2÷8= ,则DF=
,则DF= =
= ,
,
∴EF=DE+DF= ,
,
连接AE,则由圆周角性质可知:
tan∠ABF=tan∠AEF=AF:EF= .
.
分析:(1)由sinB与cosB恰好为方程mx2-mx+p-4=0的两根,sinB+cosB=1,而sin2B+cos2B=1,可得cosB=0,则∠B=90°;连接OD、OE,证明△BOE≌△DOE即可得∠OBE=∠ODE=90°;
(2)连接BD,由四边形A、B、E、F四点共圆,且∠ABE=90,得到∠ABE=∠AFE=90°,然后证明△AFD∽△ADB,从而有AF:AD=AD:AB,
(3)由sinB•cosB= =0,得p=4,即R=4,设AD=2x,则CD=3x,AC=5x,根据CD•CA=CB2,而CB2=AC2-AB2,得x=
=0,得p=4,即R=4,设AD=2x,则CD=3x,AC=5x,根据CD•CA=CB2,而CB2=AC2-AB2,得x=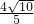 ,CB=4
,CB=4 ,DE=
,DE= CB=2
CB=2 ,又有AD2=AF•AB,即可求出AF,再由勾股定理得到DF,由此得到EF.连接AE,则tan∠ABF=tan∠AEF=AF:EF.
,又有AD2=AF•AB,即可求出AF,再由勾股定理得到DF,由此得到EF.连接AE,则tan∠ABF=tan∠AEF=AF:EF.
点评:本题考查了圆的切线的判定方法.经过半径的外端点与半径垂直的直线是圆的切线.当已知直线过圆上一点,要证明它是圆的切线,则要连接圆心和这个点,证明这个连线与已知直线垂直即可;当没告诉直线过圆上一点,要证明它是圆的切线,则要过圆心作直线的垂线,证明垂线段等于圆的半径.同时考查了三角函数、三角形相似的判定和性质以及圆的切割线定理.
∴sinB+cosB=1,
∴sin2B+2sinBcosB+cos2B=1,
又sin2B+cos2B=1,
故:sinBcosB=0,
由于∠B为三角形内角,
∴∠B≠0,
∴sinB≠0,
从而cosB=0,则∠B=90°;
连接OD、OE.如图

∵O、E分别为AB、BC的中点,
∴OE为△ABC的中位线,
则OE∥AC,
∴∠CAB=∠EOB,∠ADO=∠DOE,
由于:OA=OD,
∴∠OAD=∠ADO,
∴∠BOE=DOE,
在△BOE与△DOE中:
 ,
,∴△BOE≌△DOE,
∴∠OBE=∠ODE=90°,
∴OD⊥DE,
∴EF为⊙O的切线;
(2)解:连接BD.

∵四边形A、B、E、F四点共圆,且∠ABE=90°,
∴∠ABE=∠AFE=90°,
由EF为⊙O的切线,
∴∠ABD=∠ADF,
又∵AB为⊙O的直径,
∴∠ADB=90°=∠AFE,
∴△AFD∽△ADB,从而有AF:AD=AD:AB,
即有AD2=AF•AB;
(3)解:由于∠B=90°,
∴sinB=1,cosB=0,
∴sinB•cosB=
 =0,
=0,∵m≠0,p-4=0,
∴p=4,即R=4,
设AD=2x,则CD=3x,AC=5x,
在⊙O中,由切割线定理得:
 CD•CA=CB2,而CB2=AC2-AB2
CD•CA=CB2,而CB2=AC2-AB2∴3x•5x=(5x)2-82
∴15x2=25x2-64,
解得:x=
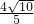 ,
,∴CB=4
 ,
,∴DE=
 CB=2
CB=2 ,
,且AD=2x=
 ,又有AD2=AF•AB,
,又有AD2=AF•AB,∴AF=(
 )2÷8=
)2÷8= ,则DF=
,则DF= =
= ,
,∴EF=DE+DF=
 ,
,连接AE,则由圆周角性质可知:
tan∠ABF=tan∠AEF=AF:EF=
 .
.分析:(1)由sinB与cosB恰好为方程mx2-mx+p-4=0的两根,sinB+cosB=1,而sin2B+cos2B=1,可得cosB=0,则∠B=90°;连接OD、OE,证明△BOE≌△DOE即可得∠OBE=∠ODE=90°;
(2)连接BD,由四边形A、B、E、F四点共圆,且∠ABE=90,得到∠ABE=∠AFE=90°,然后证明△AFD∽△ADB,从而有AF:AD=AD:AB,
(3)由sinB•cosB=
 =0,得p=4,即R=4,设AD=2x,则CD=3x,AC=5x,根据CD•CA=CB2,而CB2=AC2-AB2,得x=
=0,得p=4,即R=4,设AD=2x,则CD=3x,AC=5x,根据CD•CA=CB2,而CB2=AC2-AB2,得x=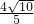 ,CB=4
,CB=4 ,DE=
,DE= CB=2
CB=2 ,又有AD2=AF•AB,即可求出AF,再由勾股定理得到DF,由此得到EF.连接AE,则tan∠ABF=tan∠AEF=AF:EF.
,又有AD2=AF•AB,即可求出AF,再由勾股定理得到DF,由此得到EF.连接AE,则tan∠ABF=tan∠AEF=AF:EF.点评:本题考查了圆的切线的判定方法.经过半径的外端点与半径垂直的直线是圆的切线.当已知直线过圆上一点,要证明它是圆的切线,则要连接圆心和这个点,证明这个连线与已知直线垂直即可;当没告诉直线过圆上一点,要证明它是圆的切线,则要过圆心作直线的垂线,证明垂线段等于圆的半径.同时考查了三角函数、三角形相似的判定和性质以及圆的切割线定理.

练习册系列答案
相关题目
 如图,已知AD为△ABC的角平分线,DE∥AB,如果
如图,已知AD为△ABC的角平分线,DE∥AB,如果 如图,已知O为△ABC的外心,AD为BC上的高,∠CAB=60°,∠ABC=44°,则∠OAD为( )
如图,已知O为△ABC的外心,AD为BC上的高,∠CAB=60°,∠ABC=44°,则∠OAD为( ) 如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,P为BC的中点.动点Q从点P出发,沿射线PC方向以2cm/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s.
如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,P为BC的中点.动点Q从点P出发,沿射线PC方向以2cm/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s. 如图,已知AD为△ABC的角平分线,AB<AC,在AC上截取CE=AB,M、N分别为BC、AE的中点.求证:MN∥AD.
如图,已知AD为△ABC的角平分线,AB<AC,在AC上截取CE=AB,M、N分别为BC、AE的中点.求证:MN∥AD.