题目内容
有3个有理数x、y、z,若x=
且x与y互为相反数,y与z为倒数.
(1)你能求出x、y、z这三个数吗?若能,请计算并写出结果;不能,请说明理由;
(2)根据(1)的结果计算:xy-yn-(y-z)2012的值.
| 2 |
| (-1)n-1 |
(1)你能求出x、y、z这三个数吗?若能,请计算并写出结果;不能,请说明理由;
(2)根据(1)的结果计算:xy-yn-(y-z)2012的值.
考点:代数式求值,有理数的混合运算
专题:
分析:(1)分为两种情况:n为奇数和偶数,求出x,即可求出y和z;
(2)把x、y、z的值代入求出即可.
(2)把x、y、z的值代入求出即可.
解答:解:(1)当n为奇数时,x=
=-1,
∵x与y互为相反数,y与z为倒数,
∴y=1,z=1;
当n为偶数时,(-1)n-1=0,此时x不存在,
即当n为奇数时,能求出x=-1,y=1,z=1;
(2)∵x=-1,y=1,z=1,
∴xy-yn-(y-z)2012=(-1)×1-1n-(1-1)2012=-2.
| 2 |
| (-1)n-1 |
∵x与y互为相反数,y与z为倒数,
∴y=1,z=1;
当n为偶数时,(-1)n-1=0,此时x不存在,
即当n为奇数时,能求出x=-1,y=1,z=1;
(2)∵x=-1,y=1,z=1,
∴xy-yn-(y-z)2012=(-1)×1-1n-(1-1)2012=-2.
点评:本题考查了有理数的乘方,相反数,倒数,求代数式的值的应用,解此题的关键是求出x、y、z的值.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
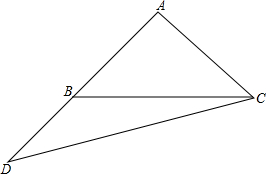 如图,在△ABC中,AB=AC,∠ABC=40°,延长AB到D,使得AD=BC,连结CD,求∠D的度数.
如图,在△ABC中,AB=AC,∠ABC=40°,延长AB到D,使得AD=BC,连结CD,求∠D的度数.