题目内容
 如图,点A、点B分别在反比例函数
如图,点A、点B分别在反比例函数 (x<0)和
(x<0)和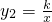 (x>0)的图象上,∠AOB恰好被y轴平分,若△OAB的面积为4,则k的值为________.
(x>0)的图象上,∠AOB恰好被y轴平分,若△OAB的面积为4,则k的值为________.
16
分析:过点A作AE⊥x轴于点E,BF⊥x轴于点F,根据∠AOB恰好被y轴平分,可判定△AOE∽△BOF,根据相似三角形的面积比等于相似比平方,可得出点A及点B坐标的关系,再由S梯形AEFB= (AE+BF)×EF=S△AEO+S△BOF+S△AOB,可得出方程,解出即可得出k的值.
(AE+BF)×EF=S△AEO+S△BOF+S△AOB,可得出方程,解出即可得出k的值.
解答:过点A作AE⊥x轴于点E,BF⊥x轴于点F,

∵∠AOB恰好被y轴平分,
∴∠AOC=∠BOC,
∵∠ACO=∠OAE,∠OBF=∠BOC,
∴∠OAE=∠OBF,
∴△AOE∽△BOF,
∴( )2=
)2= =
= (相似三角形的面积比等于相似比平方),
(相似三角形的面积比等于相似比平方),
∴ =
= ,
,
设点B的坐标为(a, ),则点A的坐标为(-
),则点A的坐标为(- a,
a, ),
),
S梯形AEFB= (AE+BF)×EF=
(AE+BF)×EF= ×(
×( +
+ )×(a+
)×(a+ a)=S△AEO+S△BOF+S△AOB=
a)=S△AEO+S△BOF+S△AOB= +
+ +4,
+4,
整理得: =4,
=4,
∵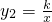 (x>0),在第一象限,
(x>0),在第一象限,
∴k>0,
∴k=16.
故答案为:16.
点评:本题考查了反比例函数的综合题,涉及了反比例函数k的几何意义、梯形及相似三角形的判定与性质,综合考察的知识点较多,注意数形结合思想的运用,将各个知识点融会贯通.
分析:过点A作AE⊥x轴于点E,BF⊥x轴于点F,根据∠AOB恰好被y轴平分,可判定△AOE∽△BOF,根据相似三角形的面积比等于相似比平方,可得出点A及点B坐标的关系,再由S梯形AEFB=
 (AE+BF)×EF=S△AEO+S△BOF+S△AOB,可得出方程,解出即可得出k的值.
(AE+BF)×EF=S△AEO+S△BOF+S△AOB,可得出方程,解出即可得出k的值.解答:过点A作AE⊥x轴于点E,BF⊥x轴于点F,

∵∠AOB恰好被y轴平分,
∴∠AOC=∠BOC,
∵∠ACO=∠OAE,∠OBF=∠BOC,
∴∠OAE=∠OBF,
∴△AOE∽△BOF,
∴(
 )2=
)2= =
= (相似三角形的面积比等于相似比平方),
(相似三角形的面积比等于相似比平方),∴
 =
= ,
,设点B的坐标为(a,
 ),则点A的坐标为(-
),则点A的坐标为(- a,
a, ),
),S梯形AEFB=
 (AE+BF)×EF=
(AE+BF)×EF= ×(
×( +
+ )×(a+
)×(a+ a)=S△AEO+S△BOF+S△AOB=
a)=S△AEO+S△BOF+S△AOB= +
+ +4,
+4,整理得:
 =4,
=4,∵
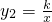 (x>0),在第一象限,
(x>0),在第一象限,∴k>0,
∴k=16.
故答案为:16.
点评:本题考查了反比例函数的综合题,涉及了反比例函数k的几何意义、梯形及相似三角形的判定与性质,综合考察的知识点较多,注意数形结合思想的运用,将各个知识点融会贯通.

练习册系列答案
相关题目
 如图,点A,B是⊙O上两点,AB=10,点P是⊙O上的动点(P与A,B不重合)连接AP,PB,过点O分别作OE⊥AP于点E,OF⊥PB于点F,则下列结论正确的是( )
如图,点A,B是⊙O上两点,AB=10,点P是⊙O上的动点(P与A,B不重合)连接AP,PB,过点O分别作OE⊥AP于点E,OF⊥PB于点F,则下列结论正确的是( )| A、EF=2.5 | ||
B、EF=
| ||
| C、EF=5 | ||
| D、EF的长度无法确定 |
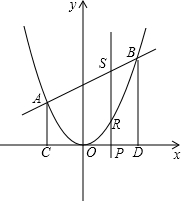 点,过点P且平行于y轴的直线与抛物线和直线分别交于R,S.
点,过点P且平行于y轴的直线与抛物线和直线分别交于R,S.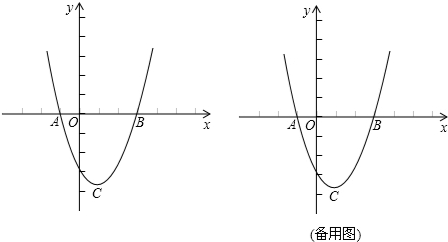
 (2013•普陀区模拟)如图,在平面直角坐标系中,矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上,OA=4,OC=2.点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段CP的中点绕点P按顺时针方向旋转90°得点D,点D随点P的运动而运动,连接DP、DA.则:
(2013•普陀区模拟)如图,在平面直角坐标系中,矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上,OA=4,OC=2.点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段CP的中点绕点P按顺时针方向旋转90°得点D,点D随点P的运动而运动,连接DP、DA.则: 如图,已知△ABC中,AB=AC=12cm,BC=10cm,点D为AB的中点.如果点P在线段BC上以2cm/s的速度由点B向C点运动,同时,点Q在线段AC 上由点A向C点以4cm/s的速度运动.
如图,已知△ABC中,AB=AC=12cm,BC=10cm,点D为AB的中点.如果点P在线段BC上以2cm/s的速度由点B向C点运动,同时,点Q在线段AC 上由点A向C点以4cm/s的速度运动.