Question

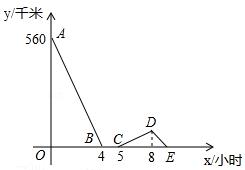
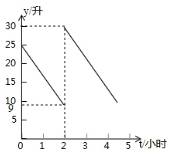
.一辆慢车与一辆快车分别从甲、乙两地同时出发，匀速相向而行，两车在途中相遇后都停留一段时间，然后分别按原速一同驶往甲地后停车．设慢车行驶的时间为x小时，两车之间的距离为y千米，图中折线表示y与x之间的函数图象，请根据图象解决下列问题：

（1）甲乙两地之间的距离为　      　千米；

（2）求快车和慢车的速度；

（3）求线段DE所表示的y与x之间的函数关系式，并写出自变量x的取值范围．

Answer 1

.解：（1）由题意可得出：甲乙两地之间的距离为560千米；故答案为：560；

（2）由题意可得出：慢车往返分别用了4小时，慢车行驶4小时的距离，快车3小时即可行驶完，

∴设慢车速度为3xkm/h，快车速度为4xkm/h，

∵由题意可得出：快车行驶全程用了7小时，∴快车速度为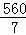：=80（km/h），

∴慢车速度为：80×=60（km/h），

（3）由题意可得出：当行驶7小时后，慢车距离甲地60km，∴D（8，60），

∵慢车往返各需4小时，∴E（9，0），设DE的解析式为：y=kx+b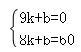，∴，解得：．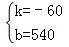

∴线段DE所表示的y与x之间的函数关系式为：y=﹣60x+540（8≤x≤9）．