题目内容
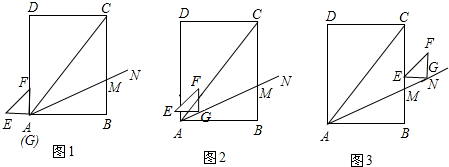
12. 数学活动课,老师和同学一起去测量校内某处的大树AB的高度,如图,老师测得大树前斜坡DE的坡度i=1:4,一学生站在离斜坡顶端E的水平距离DF为8m处的D点,测得大树顶端A的仰角为α,已知sinα=$\frac{3}{5}$,BE=1.6m,此学生身高CD=1.6m,则大树高度AB为( )m.
数学活动课,老师和同学一起去测量校内某处的大树AB的高度,如图,老师测得大树前斜坡DE的坡度i=1:4,一学生站在离斜坡顶端E的水平距离DF为8m处的D点,测得大树顶端A的仰角为α,已知sinα=$\frac{3}{5}$,BE=1.6m,此学生身高CD=1.6m,则大树高度AB为( )m.| A. | 7.4 | B. | 7.2 | C. | 7 | D. | 6.8 |
分析 根据题意结合坡度的定义得出C到AB的距离,进而利用锐角三角函数关系得出AB的长.
解答  解:如图所示:过点C作CG⊥AB延长线于点G,交EF于点N,
解:如图所示:过点C作CG⊥AB延长线于点G,交EF于点N,
由题意可得:$\frac{EF}{DF}$=$\frac{1}{4}$=$\frac{EF}{8}$,
解得:EF=2,
∵DC=1.6m,
∴FN=1.6m,
∴BG=EN=0.4m,
∵sinα=$\frac{3}{5}$=$\frac{AG}{AC}$,
∴设AG=3x,则AC=5x,
故BC=4x,即8+1.6=4x,
解得:x=2.4,
故AG=2.4×3=7.2m,
则AB=AG-BG=7.2-0.4=6.8(m),
答:大树高度AB为6.8m.
故选:D.
点评 此题主要考查了解直角三角形的应用以及坡度的定义,正确得出C到AB的距离是解题关键.

练习册系列答案
相关题目
1.一组数据5,2,3,6,8,3的中位数和众数分别是( )
| A. | 4和3 | B. | 4和8 | C. | 3和3 | D. | 5和3 |