题目内容
15．解不等式组$\left\{\begin{array}{l}{x-4≤\frac{3}{2}（2x-1），①}\\{2x-\frac{1+3x}{2}＜1，②}\end{array}\right.$把它的解集表示在数轴上，并求出不等式组的非负整数解．分析 首先解每个不等式，两个不等式的解集的公共部分就是不等式组的解集，然后确定非负整数解即可．
解答 解：解①得x≥-$\frac{5}{4}$，
解②得x＜3，
则不等式组的解集是-$\frac{5}{4}$≤x＜3．
则非负整数解是0，1，2．
点评 此题考查的是一元一次不等式组的解法．求不等式组的解集，应遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．
练习册系列答案
相关题目
3．
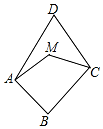如图，M是线段AD、CD的垂直平分线交点，AB⊥BC，∠D=55°，则∠MAB+∠MCB的大小是（ ）
如图，M是线段AD、CD的垂直平分线交点，AB⊥BC，∠D=55°，则∠MAB+∠MCB的大小是（ ）| A． | 120° | B． | 130° | C． | 140° | D． | 160° |
10．△ABC中，∠A=25°，∠B=87°，则∠C=（ ）
| A． | 58° | B． | 68° | C． | 78° | D． | 87° |
7．
如图，在Rt△ABC中，∠B=90°，AB=3，AC=5，点E在BC上，将△ABC沿AE折叠，使点B落在AC边上的点B′处，则BE的长为（ ）
如图，在Rt△ABC中，∠B=90°，AB=3，AC=5，点E在BC上，将△ABC沿AE折叠，使点B落在AC边上的点B′处，则BE的长为（ ）| A． | 1 | B． | $\frac{1}{2}$ | C． | $\frac{3}{2}$ | D． | 2 |