题目内容
8.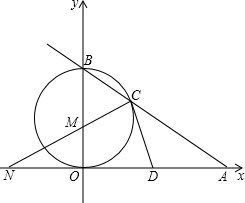 如图,已知直线AB与x轴、y轴分别交于点A和点B,OA=4,且OA,OB长是关于x的方程x2-mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM,交x轴于点N,点D为OA的中点.
如图,已知直线AB与x轴、y轴分别交于点A和点B,OA=4,且OA,OB长是关于x的方程x2-mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM,交x轴于点N,点D为OA的中点.(1)求证:CD是⊙M的切线;
(2)求线段ON的长.
分析 (1)先根据根与系数的关系求出OB的长,故可得出圆的半径.连结OC,OB是⊙M的直径,则∠ACO=90°,由D为OA的中点得出OD=AD=CD,故可得出∠OAC=∠ACD,再由∠OAC+∠OBA=90°得出∠BCM+∠ACD=90°,故∠NCD=90°,由此得出结论;
(2)根据∠CND=∠CND,∠NOM=∠NCD=90°,得出△NOM∽△NCD,再由相似三角形的对应边成比例即可得出结论.
解答 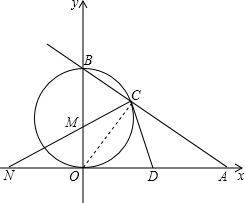 解:(1)OA、OB长是关于x的方程x2-mx+12=0的两实根,OA=4,则OA×OB=12,
解:(1)OA、OB长是关于x的方程x2-mx+12=0的两实根,OA=4,则OA×OB=12,
得OB=3,⊙M的半径为1.5;
∵BM=CM=1.5,
∴∠OBA=∠BCM.
连结OC,OB是⊙M的直径,则∠ACO=90°,D为OA的中点,
∴OD=AD=CD=2,
∴∠OAC=∠ACD,
又∵∠OAC+∠OBA=90°,
∴∠BCM+∠ACD=90°,
∴∠NCD=90°,
∴CD是⊙M的切线.
(2)∵∠CND=∠CND,∠NOM=∠NCD=90°,
∴△NOM∽△NCD,
∴$\frac{ON}{NC}$=$\frac{OM}{CD}$,即$\frac{ON}{\sqrt{(ON+2)^{2}-{2}^{2}}}$=$\frac{1.5}{2}$,
∴NO=$\frac{36}{7}$.
点评 本题考查的是圆的综合题,涉及到圆周角定理及相似三角形的判定与性质、一元二次方程的根与系数的关系,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
18.抛物线y=x2-2x+2的顶点坐标为( )
| A. | (1,1) | B. | (1,2) | C. | (-1,1) | D. | (-1,2) |
 在△ABC,∠BAC=90°,AB=AC,AD=DC,AE⊥BD,求证:∠1=∠2.
在△ABC,∠BAC=90°,AB=AC,AD=DC,AE⊥BD,求证:∠1=∠2. 如图已知直线$y=-\frac{{\sqrt{3}}}{3}x+1$与x轴和y轴分别交于点A和点B,以AB为边在第一象限内作等边三角形ABC.
如图已知直线$y=-\frac{{\sqrt{3}}}{3}x+1$与x轴和y轴分别交于点A和点B,以AB为边在第一象限内作等边三角形ABC.

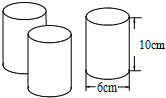 小华家来了两位客人,妈妈冲了900mL的果汁,如果用图中三个大小完全相同的玻璃杯装果汁,这些果汁能将这三个杯子装满吗?请说明理由.(π取3.14)
小华家来了两位客人,妈妈冲了900mL的果汁,如果用图中三个大小完全相同的玻璃杯装果汁,这些果汁能将这三个杯子装满吗?请说明理由.(π取3.14)