题目内容
2.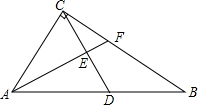 在Rt△ABC中,∠ACB=90°,AB=5,sin∠CAB=$\frac{4}{5}$,D是斜边AB上一点,过点A作AE⊥CD,垂足为E,AE的延长线交BC于点F.
在Rt△ABC中,∠ACB=90°,AB=5,sin∠CAB=$\frac{4}{5}$,D是斜边AB上一点,过点A作AE⊥CD,垂足为E,AE的延长线交BC于点F.(1)当tan∠BCD=$\frac{1}{2}$时,求线段BF的长;
(2)当BF=$\frac{5}{4}$时,求线段AD的长.
分析 (1)由题意先求出AC,BC的长,由AE⊥CD和∠ACB=90°,证明出∠CAF=∠BCD,再由tan∠BCD=$\frac{1}{2}$,可知tan∠CAF=tan∠BCD=$\frac{1}{2}$,求得CF,从而求得线段BF的长;
(2)分两种情况:①当点F在线段BC上时,根据tan∠CAF=tan∠BCD,得$\frac{CF}{AC}$=$\frac{BG}{BC}$,求出BG,由BG∥AC得$\frac{BG}{AC}=\frac{BD}{AD}$即可解决问题.②当点F在CB延长线上时,方法类似①.
解答 解:(1)在△ABC中,∠ACB=90°,AB=5,sin∠CAB=$\frac{4}{5}$,
∴BC=4,AC=3,(1分)
∵AE⊥CD,∠ACB=90°,
∴∠BCD+∠AFC=90°,∠AFC+∠CAF=90°,
∴∠CAF=∠BCD(2分)
∴tan∠CAF=tan∠BCD=$\frac{1}{2}$,
又∵∠ACB=90°,AC=3
∴CF=$\frac{3}{2}$,BF=$\frac{5}{2}$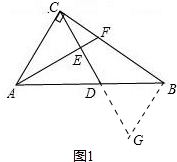
(2)①如图1中,当点F在线段BC上时,过点B作BG∥AC,交CD延长线于点G,
∵tan∠CAF=tan∠BCD,
∴$\frac{CF}{AC}$=$\frac{BG}{BC}$,即$\frac{4-BF}{3}$=$\frac{BG}{BC}$,
∴BG=$\frac{11}{3}$
∵BG∥AC
∴$\frac{BG}{AC}=\frac{BD}{AD}$,即$\frac{BG}{3}$=$\frac{5-AD}{AD}$
∴AD=$\frac{9}{4}$.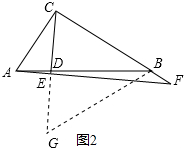 ②如图2中,当点F在CB延长线上时,过点B作BG∥AC,交CD延长线于点G,
②如图2中,当点F在CB延长线上时,过点B作BG∥AC,交CD延长线于点G,
∵tan∠CAF=tan∠BCD,
∴$\frac{CF}{AC}$=$\frac{BG}{BC}$,即$\frac{4+BF}{3}$=$\frac{BG}{BC}$,
∴BG=7,
∵BG∥AC
∴$\frac{BG}{AC}=\frac{BD}{AD}$,即$\frac{BG}{3}$=$\frac{5-AD}{AD}$
∴AD=$\frac{3}{2}$.
点评 本题主要考查了三角函数的应用、平行线分线段成比例定理,用到了分类讨论的思想,转化为方程去思考是解题的关键,是一道综合题,难度大.

| A. | y=3x | B. | y=3x-8 | C. | y=3x-16 | D. | y=3x+12 |
| A. | 4 | B. | -4 | C. | 5 | D. | -5 |
 如图,⊙O的半径为1,△ABC是⊙O的内接等边三角形,点D、E在圆上,四边形BCDE为矩形,这个矩形的面积是( )
如图,⊙O的半径为1,△ABC是⊙O的内接等边三角形,点D、E在圆上,四边形BCDE为矩形,这个矩形的面积是( )| A. | 2 | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
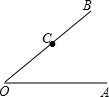 我市规划局要新建两条马路,如图所示,准备过游乐场C修一条与OA平行的马路,这条马路与∠AOB的平分线有一交点D,计划再OA边上建一个购物商场E,且使D到E最近,请利用量角器和三角板画出图形.
我市规划局要新建两条马路,如图所示,准备过游乐场C修一条与OA平行的马路,这条马路与∠AOB的平分线有一交点D,计划再OA边上建一个购物商场E,且使D到E最近,请利用量角器和三角板画出图形. 如图,平面直角坐标系中,已知y轴上有两点A、B,尺规作图作出x轴正半轴上的点P,使得∠APB最大.
如图,平面直角坐标系中,已知y轴上有两点A、B,尺规作图作出x轴正半轴上的点P,使得∠APB最大. 有一半圆片(其中圆心角∠AED=52°)在平面直角坐标系中,按如图所示放置,若点A可以沿y轴正半轴上下滑动,同时点B相应地在x轴正半轴上滑动,当∠OAB=n°时,半圆片上的点D与原点O距离最大,则n为( )°.
有一半圆片(其中圆心角∠AED=52°)在平面直角坐标系中,按如图所示放置,若点A可以沿y轴正半轴上下滑动,同时点B相应地在x轴正半轴上滑动,当∠OAB=n°时,半圆片上的点D与原点O距离最大,则n为( )°.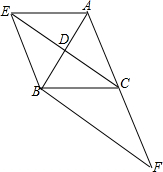 已知,如图,在三角形ABC中,CD是中线,过点A作平行线BC的平行线,交CD的延长线于点E,连接EB.
已知,如图,在三角形ABC中,CD是中线,过点A作平行线BC的平行线,交CD的延长线于点E,连接EB.