题目内容
 如图,AB为⊙O的直径,CF⊥AB于E,交⊙O于D,AF交⊙O于G.求证:∠FGD=∠ADC.
如图,AB为⊙O的直径,CF⊥AB于E,交⊙O于D,AF交⊙O于G.求证:∠FGD=∠ADC.考点:圆内接四边形的性质,垂径定理
专题:证明题
分析:利用圆内接四边形的性质求得∠FGD=∠ACD;然后根据垂径定理推知AB是CD的垂直平分线,则∠ADC=∠ACD.故:∠FGD=∠ADC.
解答:证明:∵四边形ACDG内接于⊙O,
∴∠FGD=∠ACD.
又∵AB为⊙O的直径,CF⊥AB于E,
∴AB垂直平分CD,
∴AC=AD,
∴∠ADC=∠ACD,
∴∠FGD=∠ADC.
∴∠FGD=∠ACD.
又∵AB为⊙O的直径,CF⊥AB于E,
∴AB垂直平分CD,
∴AC=AD,
∴∠ADC=∠ACD,
∴∠FGD=∠ADC.
点评:本题考查了圆内接四边形的性质和垂径定理.圆内接四边形的性质是沟通角相等关系的重要依据,在应用此性质时,要注意与圆周角定理结合起来.

练习册系列答案
相关题目
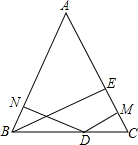 如图所示,∠B=∠C,BE⊥AC,DM⊥AC,DN⊥AB,求证:DM+DN=BE.
如图所示,∠B=∠C,BE⊥AC,DM⊥AC,DN⊥AB,求证:DM+DN=BE. 如图,在△ABC中,∠BCA=2∠A,AC=2BC,求∠ABC的度数.
如图,在△ABC中,∠BCA=2∠A,AC=2BC,求∠ABC的度数.