题目内容
20.方程x2-1=$\frac{2}{x}$的正整数解的个数是0个.分析 将方程x2-1=$\frac{2}{x}$转化为${y}_{1}={x}^{2}-1$,${y}_{2}=\frac{2}{x}$,画出函数图象,对于${y}_{2}=\frac{2}{x}$,只有当y为2和1时,x为正整数1和2,对于${y}_{1}={x}^{2}-1$,当y为2和1时,x为$±\sqrt{3}$和$±\sqrt{2}$,得到x的值不相同,所以方程x2-1=$\frac{2}{x}$的正整数解的个数是0个.
解答 解:如图,
令${y}_{1}={x}^{2}-1$,${y}_{2}=\frac{2}{x}$,
由图象可得两图象交点在第一象限,
对于${y}_{2}=\frac{2}{x}$,只有当y为2和1时,x为正整数1和2,
对于${y}_{1}={x}^{2}-1$,当y为2和1时,x为$±\sqrt{3}$和$±\sqrt{2}$,
得到x的值不相同,
∴方程x2-1=$\frac{2}{x}$的正整数解的个数是0个.
故答案为:0.
点评 本题考查了二次函数的图象,解决本题的关键是将方程转化为二次函数和反比例函数图象的交点问题.

练习册系列答案
相关题目
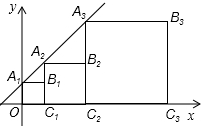 正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置,点A1、A2、A3和点C1、C2、C3、…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则B4的坐标是(15,8),B2015的坐标是(22015-1,22014).
正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置,点A1、A2、A3和点C1、C2、C3、…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则B4的坐标是(15,8),B2015的坐标是(22015-1,22014). 如图,在平行四边形ABCD中,已知AB=4,AC=3,BC=5,以BC所在的直线为y轴,以点C为原点建立平面直角坐标系.x轴交AD于点E,有一动点P以5个单位/秒的速度熊A点出发,到达B点,再到C点停止,另一动点F以3个单位/秒的速度从C点出发向x轴的正方向运动,和点P同时开始,同时停止运动,令运动的时间为t.
如图,在平行四边形ABCD中,已知AB=4,AC=3,BC=5,以BC所在的直线为y轴,以点C为原点建立平面直角坐标系.x轴交AD于点E,有一动点P以5个单位/秒的速度熊A点出发,到达B点,再到C点停止,另一动点F以3个单位/秒的速度从C点出发向x轴的正方向运动,和点P同时开始,同时停止运动,令运动的时间为t.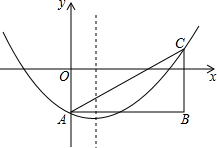 如图,在平面直角坐标系中,抛物线y=ax2-2ax-2(a>0)与y轴交于点A,点B的坐标为($\frac{1}{a}$,-2),过点B作y轴的平行线,交抛物线于点C,连结AB、AC.
如图,在平面直角坐标系中,抛物线y=ax2-2ax-2(a>0)与y轴交于点A,点B的坐标为($\frac{1}{a}$,-2),过点B作y轴的平行线,交抛物线于点C,连结AB、AC.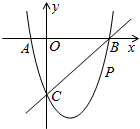 如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点左侧,B点的坐标为(4,0),与y轴交于C(0,-4)点,点P是直线BC下方的抛物线上一动点.
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点左侧,B点的坐标为(4,0),与y轴交于C(0,-4)点,点P是直线BC下方的抛物线上一动点.