题目内容
先化简,再求值:
已知|x-3|+(y+
)2=0,求3x2y-12xy2-(5x2y-8xy2)的值.
已知|x-3|+(y+
| 1 |
| 2 |
考点:整式的加减—化简求值,非负数的性质:绝对值,非负数的性质:偶次方
专题:计算题
分析:利用非负数的性质求出x与y的值,原式去括号合并后代入计算即可求出值.
解答:解:∵|x-3|+(y+
)2=0,
∴|x-3|=0,(y+
)2=0,
解得:x=3,y=-
,
原式=3x2y-12xy2-5x2y+8xy2=-2x2y-4xy2,
当x=3,y=-
时,原式=-2×32×(-
)-4×3×(-
)2=9-3=6.
| 1 |
| 2 |
∴|x-3|=0,(y+
| 1 |
| 2 |
解得:x=3,y=-
| 1 |
| 2 |
原式=3x2y-12xy2-5x2y+8xy2=-2x2y-4xy2,
当x=3,y=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查了整式的加减-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
计算2-3的结果是( )
A、
| ||
| B、-8 | ||
C、-
| ||
| D、-6 |
把二次函数y=x2-8x+7化为y=a(x-h)2+k的形式为( )
| A、y=(x+4)2-9 |
| B、y=(x-4)2+9 |
| C、y=(x-4)2-9 |
| D、y=(x+4)2+9 |
一元二次方程x2=x的根为( )
| A、0 | B、1 | C、0或1 | D、0或-1 |
下列抛物线中,与x轴无公共点的是( )
| A、y=x2-2 |
| B、y=x2+4x+4 |
| C、y=-x2+3x+2 |
| D、y=x2-x+2 |
下列美丽的图案中是轴对称图形的个数有( )


| A、1个 | B、2个 | C、3个 | D、4个 |
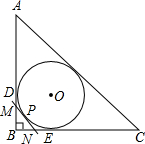 如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D、E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为4cm,则Rt△MBN的周长为
如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D、E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为4cm,则Rt△MBN的周长为