题目内容
【题目】如图，反比例函数y=
（k为常数，且k≠0）的图象x经过点A（1，4），B（2，m）．
（1）求反比例函数的解析式及B点的坐标；
（2）在y轴上找一点P，使PA+PB的值最小，求满足条件的点P的坐标．
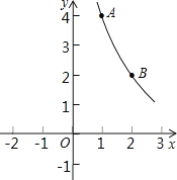
【答案】（1）y=
；B（2，2）；（2）P（0，
）．
【解析】
（1）把点A的坐标代入反比例函数解析式求得k的值，从而可得反比例函数解析式；然后将点B的坐标代入反比例函数解析式求得m的值，即可得出点B坐标；
（2）作A关于y轴的对称点
，连结
交y轴于P，此时
的值最小，再利用待定系数法求出直线的解析式，令
，即可得出点P坐标．
（1）把
代入
得
，解得
则反比例函数的解析式为
将点
代入得
则点B坐标为
；
（2）如图，作点A关于y轴的对称点，连结交y轴于P，则
由两点之间线段最短得：当点
共线时，
取得最小值，最小值为
即当点P为直线与y轴的交点时，的值最小
设直线的解析式为
把
代入得
，
解得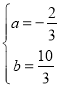
则设直线的解析式为
令得
故满足条件的点P的坐标为
．
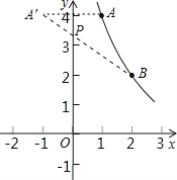
练习册系列答案
相关题目
