题目内容
 如图,已知双曲线y=
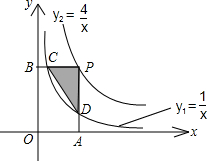
如图,已知双曲线y= (x>0)经过矩形OABC的边AB、BC上的点F、E,其中CE=
(x>0)经过矩形OABC的边AB、BC上的点F、E,其中CE= CB,AF=
CB,AF= AB,且四边形OEBF的面积为2,则k的值为
AB,且四边形OEBF的面积为2,则k的值为
- A.1
- B.

- C.2
- D.

A
分析:设矩形的长为a,宽为b,则由已知表示出矩形的面积,△COE和△AOF的面积及四边形OEBF的面积,从而求出三角形AOF的面积,则求出k的值.
解答:设矩形的长为a,宽为b,
则由CE= CB,AF=
CB,AF= AB,得:
AB,得:
CE= a,AF=
a,AF= b,
b,
∴△COE的面积为: ab,
ab,
△AOF的面积为: ab,
ab,
矩形的面积为:ab,
四边形OEBF的面积为:ab- ab-
ab- ab=
ab= ab,
ab,
∴△AOF的面积:四边形OEBF的面积= :
: =1:4,
=1:4,
∴△AOF的面积=四边形OEBF的面积× =2×
=2× =
= ,
,
∴ |k|=
|k|= ,
,
又由于反比例函数的图象位于第一象限,k>0;
∴k=1.
故选A.
点评:本题主要考查了反比例函数y= 中k的几何意义.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.
中k的几何意义.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.
分析:设矩形的长为a,宽为b,则由已知表示出矩形的面积,△COE和△AOF的面积及四边形OEBF的面积,从而求出三角形AOF的面积,则求出k的值.
解答:设矩形的长为a,宽为b,
则由CE=
 CB,AF=
CB,AF= AB,得:
AB,得:CE=
 a,AF=
a,AF= b,
b,∴△COE的面积为:
 ab,
ab,△AOF的面积为:
 ab,
ab,矩形的面积为:ab,
四边形OEBF的面积为:ab-
 ab-
ab- ab=
ab= ab,
ab,∴△AOF的面积:四边形OEBF的面积=
 :
: =1:4,
=1:4,∴△AOF的面积=四边形OEBF的面积×
 =2×
=2× =
= ,
,∴
 |k|=
|k|= ,
,又由于反比例函数的图象位于第一象限,k>0;
∴k=1.
故选A.
点评:本题主要考查了反比例函数y=
 中k的几何意义.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.
中k的几何意义.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义. 
练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 如图,已知双曲线
如图,已知双曲线 (2012•济南)如图,已知双曲线y=
(2012•济南)如图,已知双曲线y= (2013•徐州模拟)如图,已知双曲线y=
(2013•徐州模拟)如图,已知双曲线y= 如图,已知双曲线
如图,已知双曲线 如图,已知双曲线
如图,已知双曲线