题目内容
已知抛物线y=k(x+1)(x- )与x轴交于点A,B,与y轴交于点C,则能使△ABC为等腰三角形的抛物线的条数是( )
)与x轴交于点A,B,与y轴交于点C,则能使△ABC为等腰三角形的抛物线的条数是( )
A.2 B.3 C.4 D.5
C 解析:令y=0,则k(x+1)(x- )=0,解得x1=-1,x2=
)=0,解得x1=-1,x2= ,设A点坐标 为(-1,0),则B点的坐标为(
,设A点坐标 为(-1,0),则B点的坐标为( ,0).
,0).
当x=0时,y=-3,∴C(0,-3),AC=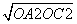 =
=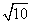 .
.
(1)k>0时,有以下3种情况:①当AC=BC时,点A、B分别在x轴的负半轴和正半轴上,且AO=BO,即1= ,解得k=3;②当AB=BC时,AB2=B
,解得k=3;②当AB=BC时,AB2=B C2=BO2+CO2,即(
C2=BO2+CO2,即( +1)2=(
+1)2=( )2+32,
)2+32, 解得k=
解得k=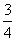 ;③当AB=AC时,AB2=AC2,即(
;③当AB=AC时,AB2=AC2,即( +1)2=10,解得k=
+1)2=10,解得k=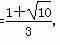 (k>0,舍去k=
(k>0,舍去k=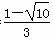 ).
).
(2)k<0时,点B只能在点A的左侧.只有当AB=AC时,△ABC可构成等腰三角形,∴- -1=
-1=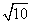 ,解得k=
,解得k=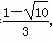 ,综上可知,当k1=3,k2=
,综上可知,当k1=3,k2=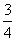 ,k3=
,k3=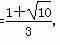 ,k4=
,k4=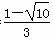 时,△ABC为等腰三角形,故能使△ABC为等腰三角形的抛物线的条数是4.
时,△ABC为等腰三角形,故能使△ABC为等腰三角形的抛物线的条数是4.

练习册系列答案
相关题目
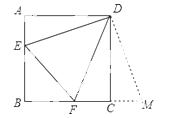
 点E是BC边上的点,∠AEP=90°,且EP交正方形外角的平分线CP于点P,交边CD于点F,
点E是BC边上的点,∠AEP=90°,且EP交正方形外角的平分线CP于点P,交边CD于点F,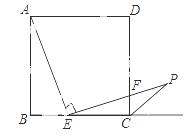

 的图象经过点(-1,-2),则k的值是( )
的图象经过点(-1,-2),则k的值是( ) =2x-6与反比例函数y=
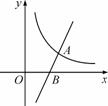
=2x-6与反比例函数y= (x>0)的图象交于点A(4,2),与x轴交于点B.
(x>0)的图象交于点A(4,2),与x轴交于点B.