题目内容
14. 如图,直线l过正方形ABCD顶点B,点A、C到直线l距离分别是1和2,求正方形边长.
如图,直线l过正方形ABCD顶点B,点A、C到直线l距离分别是1和2,求正方形边长.
分析 过点A、C分别向直线l作垂线段,根据AAS证明△ABE≌△CBF解答即可.
解答 解: 过点A、C分别向直线l作垂线段,垂足是E、F,则
过点A、C分别向直线l作垂线段,垂足是E、F,则
由题可知,AE=1,CF=2,∠AEB=∠CFB=90°,
∴∠ABE+∠BAE=90°,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠ABE+∠CBF=90°,
∴∠CBF=∠BAE
在△ABE与△CBF中
$\left\{\begin{array}{l}{∠CBF=∠BAE}\\{∠AEB=∠BFC}\\{AB=BC}\end{array}\right.$,
∴△ABE≌△CBF(AAS),
∴BE=CF=2,
在Rt△ABE中,$AB=\sqrt{A{E}^{2}+B{E}^{2}}=\sqrt{{1}^{2}+{2}^{2}}=\sqrt{5}$.
点评 本题考查了全等三角形的判定与性质,正方形的性质,熟记三角形的判定方法是解题的关键,要注意AAS证明△ABE≌△CBF.

练习册系列答案
相关题目
4.下列图形都是由几个黑色和白色的正方形按一定规律组成,图①中有2个黑色正方形,图②中有5个黑色正方形,图③中有8个黑色正方形,图④中有11个黑色正方形,…,依次规律,图10中黑色正方形的个数是29.


2.下列必然发生的事件是( )
| A. | 明天会下雨 | B. | 小红数学考试得了120分 | ||
| C. | 今天是31号,明天是1号 | D. | 2013年有366天 |
9.点P(2,-3)关于原点对称的点的坐标是( )
| A. | (-2,-3) | B. | (2,3) | C. | (-2,3) | D. | (-3,2) |
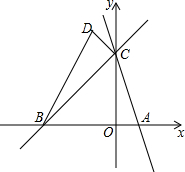 如图:直线y=-3x+3与x轴交于点A,与y轴交于点C,直线BC与x轴交于B(-3,0),与y轴交于点C.
如图:直线y=-3x+3与x轴交于点A,与y轴交于点C,直线BC与x轴交于B(-3,0),与y轴交于点C.