题目内容
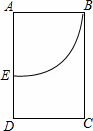
如图,反比例函数y=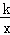 (k<0)的图象与矩形ABCD的边相交于E、F两点,且BE=2AE,E(﹣1,2).
(k<0)的图象与矩形ABCD的边相交于E、F两点,且BE=2AE,E(﹣1,2).
(1)求反比例函数的解析式;
(2)连接EF,求△BEF的面积.

解:(1)∵反比例函数y= (k<0)的图象过点E(﹣1,2),
(k<0)的图象过点E(﹣1,2),
∴k=﹣1×2=﹣2,
∴反比例函数的解析式为y=﹣ ;
;
(2)∵E(﹣1,2),
∴AE=1,OA=2,
∴BE=2AE=2,
∴AB=AE+BE=1+2=3,
∴B(﹣3,2).
将x=﹣3代入y=﹣ ,得y=
,得y= ,
,
∴CF= ,
,
∴BF=2﹣ =
= ,
,
∴△BEF的面积= BE•BF=
BE•BF= ×2×
×2× =
= .
.

练习册系列答案
相关题目
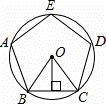
如图,⊙O是正五边形ABCDE的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是( )
|
| A. | R2﹣r2=a2 | B. | a=2Rsin36° | C. | a=2rtan36° | D. | r=Rcos36° |
 B.
B. C.
C. D.
D.
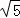 ﹣1.其中正确的说法是 .(把你认为正确的说法的序号都填上)
﹣1.其中正确的说法是 .(把你认为正确的说法的序号都填上)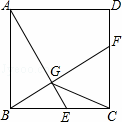

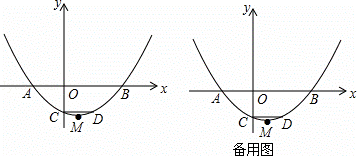
 (x+2)(x﹣4)与x轴交于点A、B(点A位于点B的左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.
(x+2)(x﹣4)与x轴交于点A、B(点A位于点B的左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.