题目内容
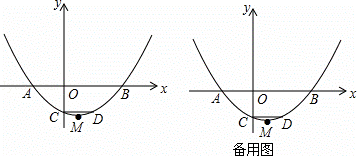
如图,已知抛物线y=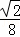 (x+2)(x﹣4)与x轴交于点A、B(点A位于点B的左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.
(x+2)(x﹣4)与x轴交于点A、B(点A位于点B的左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.
(1)求点A、B、C的坐标;
(2)设动点N(﹣2,n),求使MN+BN的值最小时n的值;
(3)P是抛物线上一点,请你探究:是否存在点P,使以P、A、B为顶点的三角形与△ABD相似(△PAB与△ABD不重合)?若存在,求出点P的坐标;若不存在,说明理由.
解:(1)令y=0得x1=﹣2,x2=4,
∴点A(﹣2,0)、B(4,0)
令x=0得y=﹣ ,
,
∴点C(0,﹣ )
)
(2)将x=1代入抛物线的解析式得y=﹣
∴点M的坐标为(1,﹣ )
)
∴点M关于直线x=﹣2的对称点M′的坐标为(﹣5, )
)
设直线M′B的解析式为y=kx+b
将点M′、B的坐标代入得:
解得:
所以直线M′B的解析式为y= .
.
将x=﹣2代入得:y=﹣
所以n=﹣ .
.
(3)过点D作DE⊥BA,垂足为E.

由勾股定理得:
AD= =3
=3 ,
,
BD= ,
,
如下图,①当P1AB∽△ADB时,
 即:
即:
∴P1B=6
过点P1作P1M1⊥AB,垂足为M1.
∴ 即:
即:
解得:P1M1=6 ,
,
∵ 即:
即:
解得:BM1=12
∴点P1的坐标为(﹣8,6 )
)
∵点P1不在抛物线上,所以此种情况不存在;
②当△P2AB∽△BDA时, 即:
即:
∴P2B=6
过点P2作P2M2⊥AB,垂足为M2.
∴ ,即:
,即:
∴P2M2=2
∵ ,即:
,即:
∴M2B=8
∴点P2的坐标为(﹣4,2 )
)
将x=﹣4代入抛物线的解析式得:y=2 ,
,
∴点P2在抛物线上.
由抛物线的对称性可知:点P2与点P4关于直线x=1对称,
∴P4的坐标为(6,2 ),
),
当点P3位于点C处时,两三角形全等,所以点P3的坐标为(0,﹣ ),
),
综上所述点P的坐标为:(﹣4,2 )或(6,2
)或(6,2 )或(0,﹣
)或(0,﹣ )时,以P、A、B为顶点的三角形与△ABD相似.
)时,以P、A、B为顶点的三角形与△ABD相似.

某校九年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛预赛.各参赛选手的成绩如图:
九(1)班:88,91,92,93,93,93,94,98,98,100
九(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
| 班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
| 九(1)班 | 100 | m | 93 | 93 | 12 |
| 九(2)班 | 99 | 95 | n | 93 | 8.4 |
(1)直接写出表中m、n的值;
(2)依据数据分析表,有人说:“最高分在(1)班,(1)班的成绩比(2)班好”,但也有人说(2)班的成绩要好,请给出两条支持九(2)班成绩好的理由;
(3)若从两班的参赛选手中选四名同学参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在四个“98分”的学生中任选二个,试求另外两个决赛名额落在同一个班的概率.
某班组织了一次读书活动,统计了10名同学在一周内的读书时间,他们一周内的读书时间累计如表,则这10名同学一周内累计读书时间的中位数是( )
| 一周内累计的读书时间(小时) | 5 | 8 | 10 | 14 |
| 人数(个) | 1 | 4 | 3 | 2 |
|
| A. | 8 | B. | 7 | C. | 9 | D. | 10 |
 的分式方程
的分式方程 有增根,则
有增根,则 的值是
的值是 B.
B. C.
C. D.
D.

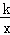 (k<0)的图象与矩形ABCD的边相交于E、F两点,且BE=2AE,E(﹣1,2).
(k<0)的图象与矩形ABCD的边相交于E、F两点,且BE=2AE,E(﹣1,2).
 的图象有一支位于第一象限,则常数a的取值范围是
的图象有一支位于第一象限,则常数a的取值范围是 