题目内容
16. 一个涵洞成抛物线形,它的截面如图,现测得:当水面宽AB=1.6m时,涵洞顶点与水面的距离为2.4m,离开水面1.5m处是涵洞宽ED.
一个涵洞成抛物线形,它的截面如图,现测得:当水面宽AB=1.6m时,涵洞顶点与水面的距离为2.4m,离开水面1.5m处是涵洞宽ED.(1)求抛物线的解析式;
(2)求ED的长.
分析 (1)根据这个函数过原点,那么可设为y=kx2,有CO和AB的长,那么点A的坐标应该是(-0.8,-2.4),利用待定系数法即可解决;
(2)根据题意令y=-(2.4-1.5),求出x的值即可得.
解答 解:(1)设为y=kx2,
由CO和AB的长,那么A的坐标应该是(-0.8,-2.4),
将其代入函数中得:-2.4=0.8×0.8×k,
解得k=-$\frac{15}{4}$.
那么函数的解析式就是:y=-$\frac{15}{4}$x2;
(2)根据题意,当y=-0.9时,-$\frac{15}{4}$x2=-0.9,
解得:x=±$\frac{\sqrt{6}}{5}$,
∴ED=$\frac{2\sqrt{6}}{5}$.
点评 本题考查了用待定系数法求二次函数的解析式,根据图中信息得出函数经过的点的坐标是解题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
6.下列方程中,是关于x的一元二次方程的是( )
| A. | x2+$\frac{1}{{x}^{2}}$=1 | B. | x2+3x-1=0 | C. | ax2+bx+c | D. | 3x+y=10 |
5.在2016年“十一”黄金周期间,南京博物馆迎来观众34000人,这个数可用科学记数法表示为( )
| A. | 3.4×103 | B. | 34×103 | C. | 0.34×103 | D. | 3.4×104 |
 有理数a、b、c在数轴上的位置如图所示,化简|a+c|+|b+c|-|b-a|.
有理数a、b、c在数轴上的位置如图所示,化简|a+c|+|b+c|-|b-a|.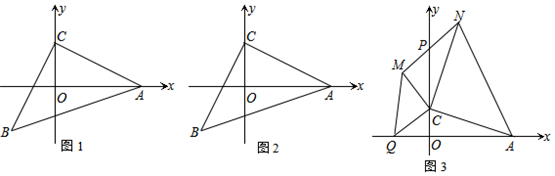
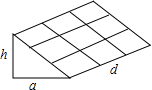 如图,要修建一个育苗棚,棚高h=3m,棚宽a=4m,棚长d=12m,现要在育苗棚的整个表面(除底面外所有的面)覆盖一层塑料薄膜,试求至少需要多少平方米塑料薄膜?(接缝处不计)
如图,要修建一个育苗棚,棚高h=3m,棚宽a=4m,棚长d=12m,现要在育苗棚的整个表面(除底面外所有的面)覆盖一层塑料薄膜,试求至少需要多少平方米塑料薄膜?(接缝处不计)