Question

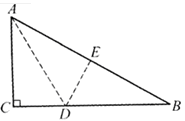
如图所示的三角形纸片中∠B=90°，AC=13，BC=5．现将纸片进行折叠，使得顶点D落在AC边上，折痕为AE．则BE的长为（ ）

A．2.4
B．2.5
C．2.8
D．3

Answer 1

【答案】分析：由∠B=90°，AC=13，BC=5，可求得AB的长，设BE=x，由折叠的性质可得：△DEC是直角三角形，ED=BE=x，EC=5-x，CD=1，然后由勾股定理求得BE的长．
解答：解：∵∠B=90°，AC=13，BC=5，
∴AB==12，
设BE=x，
由折叠的性质可得：CD=AC-AD=13-12=1，DE=BE=x，∠ADE=∠B=90°，
∴EC=BC-BE=5-x，
在Rt△DEC中，EC²=CD²+DE²，
∴（5-x）²=1+x²，
解得：x=2.4，
∴BE=2.4．
故选A．
点评：此题考查了折叠的性质以及勾股定理．此题难度适中，注意掌握折叠前后图形的对应关系，注意数形结合思想与方程思想的应用．