题目内容
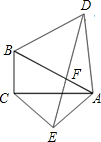 如图,已知在直角三角形ABC中,∠BCA=90°,cos∠BAC=
如图,已知在直角三角形ABC中,∠BCA=90°,cos∠BAC=| 4 |
| 5 |
(1)求
| S△ADB |
| S△AEC |
(3)求
| AF |
| FB |
考点:相似三角形的判定与性质,等腰直角三角形,平行四边形的判定与性质,解直角三角形
专题:几何综合题
分析:(1)先根据∠DAC=∠BAE=90°,得出∠DAB=∠EAC,再根据AD=BD,AE=EC,得出∠DBA=∠ECA,从而证出△ADB∽△AEC,得出
=(
)2,最后根据cos∠BAC=
=
,即可求出
的值;
(2)先过点E作EH⊥AC,延长交AB于G,连接DG,得出AH=CH,EH⊥AC,根据∠BCA=90°,证出GH∥BC,AG=BG,再根据AD=BD,得出DG⊥AB,最后根据AD⊥AC,AE⊥AB,得出GE∥AD,DG∥AE,
从而证出四边形ADGE是平行四边形,得出AF=GF,即可求出答案.
| S△ADB |
| S△AEC |
| AB |
| AC |
| 4 |
| 5 |
| AC |
| AB |
| S△ADB |
| S△AEC |
(2)先过点E作EH⊥AC,延长交AB于G,连接DG,得出AH=CH,EH⊥AC,根据∠BCA=90°,证出GH∥BC,AG=BG,再根据AD=BD,得出DG⊥AB,最后根据AD⊥AC,AE⊥AB,得出GE∥AD,DG∥AE,
从而证出四边形ADGE是平行四边形,得出AF=GF,即可求出答案.
解答: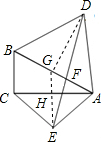 证明:(1)∵AD⊥AC,AE⊥AB,
证明:(1)∵AD⊥AC,AE⊥AB,
∴∠DAC=∠BAE=90°,
∴∠DAB=∠EAC,
∵AD=BD,AE=EC,
∴∠DAB=∠DBA,∠ECA=∠EAC,
∴∠DBA=∠ECA,
∴△ADB∽△AEC,
∴
=(
)2,
∵∠BCA=90°,
cos∠BAC=
=
,
∴
=
;
(2)过点E作EH⊥AC,延长交AB于G,连接DG,
∵AE=EC,
∴AH=CH,EH⊥AC,
∵∠BCA=90°,
∴GH∥BC,
∴AG=BG,
∵AD=BD,
∴DG⊥AB,
∵AD⊥AC,AE⊥AB,
∴GE∥AD,DG∥AE,
∴四边形ADGE是平行四边形,
∴AF=GF,
∴
=
.
 证明:(1)∵AD⊥AC,AE⊥AB,
证明:(1)∵AD⊥AC,AE⊥AB,∴∠DAC=∠BAE=90°,
∴∠DAB=∠EAC,
∵AD=BD,AE=EC,
∴∠DAB=∠DBA,∠ECA=∠EAC,
∴∠DBA=∠ECA,
∴△ADB∽△AEC,
∴
| S△ADB |
| S△AEC |
| AB |
| AC |
∵∠BCA=90°,
cos∠BAC=
| 4 |
| 5 |
| AC |
| AB |
∴
| S△ADB |
| S△AEC |
| 25 |
| 16 |
(2)过点E作EH⊥AC,延长交AB于G,连接DG,
∵AE=EC,
∴AH=CH,EH⊥AC,
∵∠BCA=90°,
∴GH∥BC,
∴AG=BG,
∵AD=BD,
∴DG⊥AB,
∵AD⊥AC,AE⊥AB,
∴GE∥AD,DG∥AE,
∴四边形ADGE是平行四边形,
∴AF=GF,
∴
| AF |
| FB |
| 1 |
| 3 |
点评:此题考查了相似三角形的判定与性质,用到的知识点是等腰三角形的性质,平行四边形的判定与性质和解直角三角形,解题的关键是根据相似三角形的判定证出△ADB∽△AEC.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知分数a的分母是2012,分子是整数,为使|
-a|的数值最小,a的分子应当是( )
| 3 |
| 5 |
| A、1206 | B、1207 |
| C、1205 | D、1208 |
 星期六,同学们可以休息了,有的同学搭顺路的大客车回家,其中一个同学画了一张图如图,由图可判断大客车驶向
星期六,同学们可以休息了,有的同学搭顺路的大客车回家,其中一个同学画了一张图如图,由图可判断大客车驶向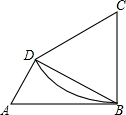 如图,有一四边形形状的铁皮ABCD,BC=CD=12,AB=2AD,∠ABC=∠ADB=90°,以C为圆心,CB为半径作弧BD得一扇形CBD,剪下扇形并用它围成一圆锥的侧面.则该圆锥的底面半径为
如图,有一四边形形状的铁皮ABCD,BC=CD=12,AB=2AD,∠ABC=∠ADB=90°,以C为圆心,CB为半径作弧BD得一扇形CBD,剪下扇形并用它围成一圆锥的侧面.则该圆锥的底面半径为 如图是一组数据的折线统计图,这组数据的方差是
如图是一组数据的折线统计图,这组数据的方差是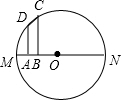 如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD=2,AB=1,BC=3.若此梯形的顶点A、B恰好在圆O的直径MN上,C、D在圆O上,则圆O的直径等于
如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD=2,AB=1,BC=3.若此梯形的顶点A、B恰好在圆O的直径MN上,C、D在圆O上,则圆O的直径等于
