题目内容
9. 如图,直线a∥b,c∥d,∠1=56°,则∠2等于( )
如图,直线a∥b,c∥d,∠1=56°,则∠2等于( )| A. | 56° | B. | 112° | C. | 124° | D. | 134° |
分析 根据平行线的性质得到∠3=∠1,∠2+∠3=180°,即可得到结论.
解答  解:∵a∥b,
解:∵a∥b,
∴∠3=∠1=56°,
又∵c∥d,
∴∠2=180°-∠3=180°-56°=124°,
故选:C.
点评 本题考查了平行线的性质,解题时注意:运用两直线平行,内错角相等是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.3-2是( )
| A. | -6 | B. | $\frac{1}{9}$ | C. | 9 | D. | $\frac{1}{6}$ |
17.计算(-2a2)2•a,正确的是( )
| A. | 2a5 | B. | -4a5 | C. | 4a5 | D. | 4a6 |
4.|2-5|=( )
| A. | -7 | B. | 7 | C. | -3 | D. | 3 |
14.2016年我国国内生产总值达到74.4万亿元,比上年增长6.7%.将74.4万亿用科学记数法表示为( )
| A. | 74.4×1012 | B. | 7.44×1012 | C. | 0.744×1013 | D. | 7.44×1013 |
1.一家鞋店在某段时间统计了某种女鞋不同尺寸的销售数据如下表,则该店最关注的应该是这组数据的( )
| 尺寸/cm | 22 | 22.5 | 23 | 23.5 | 24 | 24.5 | 25 |
| 销售量(双) | 1 | 2 | 5 | 11 | 7 | 3 | 1 |
| A. | 方差 | B. | 众数 | C. | 平均数 | D. | 频数 |
18.方程$\frac{{x}^{2}-1}{x+1}$=0的解是( )
| A. | 无解 | B. | x=1 | C. | x=-1 | D. | x=±1 |
19.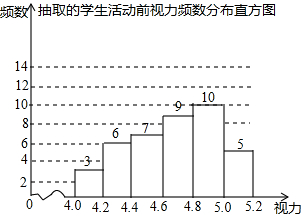 为了保护视力,学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示(数据包括左端点不包括右端点,精确到0.1);活动后,再次检查这部分学生的视力,结果如表所示
为了保护视力,学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示(数据包括左端点不包括右端点,精确到0.1);活动后,再次检查这部分学生的视力,结果如表所示
(1)求活动所抽取的学生人数;
(2)若视力达到4.8及以上为达标,计算活动前该校学生的视力达标率;
(3)请选择适当的统计量,从两个不同的角度评价视力保健活动的效果.
 为了保护视力,学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示(数据包括左端点不包括右端点,精确到0.1);活动后,再次检查这部分学生的视力,结果如表所示
为了保护视力,学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示(数据包括左端点不包括右端点,精确到0.1);活动后,再次检查这部分学生的视力,结果如表所示 | 分组 | 频数 |
| 4.0≤x<4.2 | 2 |
| 4.2≤x<4.4 | 3 |
| 4.4≤x<4.6 | 5 |
| 4.6≤x<4.8 | 8 |
| 4.8≤x<5.0 | 17 |
| 5.0≤x<5.2 | 5 |
(2)若视力达到4.8及以上为达标,计算活动前该校学生的视力达标率;
(3)请选择适当的统计量,从两个不同的角度评价视力保健活动的效果.
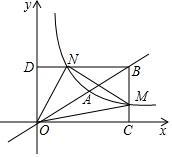 如图,矩形OCBD的顶点O与坐标原点重合,点C在x轴上,点A在对角线OB上,且OA=$\sqrt{5}$,tan∠BOC=$\frac{1}{2}$.反比例函数y=$\frac{k}{x}$的图象经过点A,交BC、BD于点M、N,CM=$\frac{2}{3}$,连接OM、ON、MN.
如图,矩形OCBD的顶点O与坐标原点重合,点C在x轴上,点A在对角线OB上,且OA=$\sqrt{5}$,tan∠BOC=$\frac{1}{2}$.反比例函数y=$\frac{k}{x}$的图象经过点A,交BC、BD于点M、N,CM=$\frac{2}{3}$,连接OM、ON、MN.