题目内容
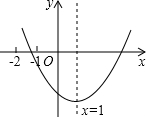 已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列结论:①b2-4ac>0;②abc>0;③a-b+c>0;④4a+2b+c<0.
其中,正确结论的个数是( )
| A、1 | B、2 | C、3 | D、4 |
考点:二次函数图象与系数的关系
专题:
分析:由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点得出c的值,然后根据抛物线与x轴交点的个数及x=-1时,x=0时二次函数的值的情况及抛物线的对称性进行推理,进而对所得结论进行判断.
解答:解:由抛物线与x轴有两个交点可以看出方程ax2+bx+c=0的根的判别式b2-4ac>0,故①正确;
由二次函数的图象开口向上可得a>0,根据二次函数的图象与y轴交于负半轴知:c<0,由对称轴为直线x=1,可得出b与a异号,即b<0,则abc>0,故②正确;
把x=-1代入y=ax2+bx+c得:y=a-b+c,由函数图象可以看出当x=-1时,二次函数的值为负,即a+b+c<0,故③错误;
把x=2代入y=ax2+bx+c得:y=4a+2b+c,由抛物线的对称性可知x=2与x=0时的函数值相等,所以4a+2b+c<0,故④正确;
故选:C.
由二次函数的图象开口向上可得a>0,根据二次函数的图象与y轴交于负半轴知:c<0,由对称轴为直线x=1,可得出b与a异号,即b<0,则abc>0,故②正确;
把x=-1代入y=ax2+bx+c得:y=a-b+c,由函数图象可以看出当x=-1时,二次函数的值为负,即a+b+c<0,故③错误;
把x=2代入y=ax2+bx+c得:y=4a+2b+c,由抛物线的对称性可知x=2与x=0时的函数值相等,所以4a+2b+c<0,故④正确;
故选:C.
点评:本题考查二次函数图象与二次函数系数之间的关系,二次函数与方程之间的转换,根的判别式的熟练运用.会利用特殊值代入法求得特殊的式子,如:y=a+b+c,y=4a+2b+c,然后根据图象判断其值.

练习册系列答案
相关题目
已知?ABCD中,∠A+∠C=240°,则∠B的度数是( )
| A、100° | B、60° |
| C、80° | D、160° |
已知两条线段长分别为
,
,那么能与它们组成直角三角形的第三条线段长是( )
| 5 |
| 7 |
A、
| ||||
B、2
| ||||
| C、12 | ||||
D、
|
若|x-2|+(3y+2)2=0,则(x+1)y的值是( )
| A、-1 | ||
| B、-2 | ||
| C、-3 | ||
D、
|
已知:平行四边形ABCD中,AB=8,则对角线的长为( )
| A、6和8 | B、10和8 |
| C、4和10 | D、6和10 |
下列各式计算正确的是( )
| A、(a2)4=(a4)2 |
| B、2x3•5x2=10x6 |
| C、(-c)8÷(-c)6=-c2 |
| D、(ab3)2=ab6 |
 如图,△ABC中,∠ACB=90°,CD⊥AB交AB于点D,∠A=30°,BD=1.5cm,则AD=
如图,△ABC中,∠ACB=90°,CD⊥AB交AB于点D,∠A=30°,BD=1.5cm,则AD= 如图,直线y=kx+b经过点A(0,5),B(1,4).
如图,直线y=kx+b经过点A(0,5),B(1,4).