题目内容
7.化简或计算(1)$\frac{2y}{x-y}$•$\frac{{x}^{2}-{y}^{2}}{{y}^{2}}$
(2)$\frac{x}{{x}^{2}-1}$+$\frac{3x+1}{{x}^{2}-1}$+$\frac{2x+3}{1-{x}^{2}}$
(3)$\frac{x+y}{xy}$-$\frac{y+z}{yz}$
(4)($\frac{3x}{x-2}$-$\frac{x}{x+2}$)÷$\frac{x}{{x}^{2}-4}$.
分析 (1)原式约分即可得到结果;
(2)原式变形后,利用同分母分式的加减法则计算即可得到结果;
(3)原式通分并利用同分母分式的减法法则计算即可得到结果;
(4)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果.
解答 解:(1)原式=$\frac{2y}{x-y}$•$\frac{(x+y)(x-y)}{{y}^{2}}$=$\frac{2(x+y)}{y}$;
(2)原式=$\frac{x+3x+1-2x-3}{(x+1)(x-1)}$=$\frac{2(x-1)}{(x+1)(x-1)}$=$\frac{2}{x+1}$;
(3)原式=$\frac{xz+yz}{xyz}$-$\frac{xy+xz}{xyz}$=$\frac{xz+yz-xy-xz}{xyz}$=$\frac{y(z-x)}{xyz}$=$\frac{z-x}{xz}$;
(4)原式=$\frac{3{x}^{2}+6x-{x}^{2}+2x}{(x+2)(x-2)}$•$\frac{(x+2)(x-2)}{x}$=2x+8.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
12.下列四幅汽车标志,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
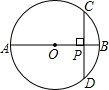 如图,AB是⊙O的直径,弦CD⊥AB,垂足为P.若CD=8,OP=3,则⊙O的半径为5.
如图,AB是⊙O的直径,弦CD⊥AB,垂足为P.若CD=8,OP=3,则⊙O的半径为5. 如图,给出三个等量关系:①AD=BC ②∠D=∠C③∠DAB=∠CBA,请你以其中两个为条件,另一个为结论,写出所有真命题(写成“已知…,求证…”的形式),并选其中一个加以证明.
如图,给出三个等量关系:①AD=BC ②∠D=∠C③∠DAB=∠CBA,请你以其中两个为条件,另一个为结论,写出所有真命题(写成“已知…,求证…”的形式),并选其中一个加以证明.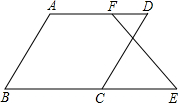 在括号内填写理由.
在括号内填写理由.