题目内容
17.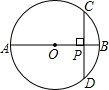 如图,AB是⊙O的直径,弦CD⊥AB,垂足为P.若CD=8,OP=3,则⊙O的半径为5.
如图,AB是⊙O的直径,弦CD⊥AB,垂足为P.若CD=8,OP=3,则⊙O的半径为5.
分析 连接OC,先根据垂径定理求出PC的长,再根据勾股定理求出OC的长即可.
解答  解:连接OC.
解:连接OC.
∵AB⊥CD,CD=8,
∴PC=$\frac{1}{2}$CD=4,
∴OC=$\sqrt{{OP}^{2}+{PC}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5.
故答案为:5.
点评 本题考查的是垂径定理,熟知平分弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.已知M(1,2),则M关于原点的对称点N落在( )
| A. | y=$\frac{1}{x}$的图象上 | B. | y=-$\frac{1}{x}$的图象上 | C. | y=$\frac{2}{x}$的图象上 | D. | y=-$\frac{2}{x}$的图象上 |
9. 一副三角板有两个三角形,如图叠放在一起,则∠α的度数是( )
一副三角板有两个三角形,如图叠放在一起,则∠α的度数是( )
 一副三角板有两个三角形,如图叠放在一起,则∠α的度数是( )
一副三角板有两个三角形,如图叠放在一起,则∠α的度数是( )| A. | 120° | B. | 135° | C. | 150° | D. | 165° |
6.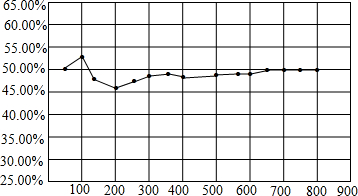 在对某次实验数据整理过程中,某个事件出现的频率随实验次数变化析线图如图所示,则符合这一结果的实验最有可能的是( )
在对某次实验数据整理过程中,某个事件出现的频率随实验次数变化析线图如图所示,则符合这一结果的实验最有可能的是( )
 在对某次实验数据整理过程中,某个事件出现的频率随实验次数变化析线图如图所示,则符合这一结果的实验最有可能的是( )
在对某次实验数据整理过程中,某个事件出现的频率随实验次数变化析线图如图所示,则符合这一结果的实验最有可能的是( )| A. | 抛一个质地均匀的正六面体骰子,向上的面点数是4 | |
| B. | 暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球 | |
| C. | 一副的普通扑克牌洗匀后,从中任取一张牌的花色是红桃 | |
| D. | 抛硬币实验中关注正面出现的概率 |
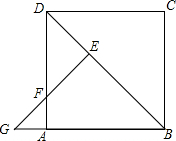 如图,连接正方形ABCD的对角线BD,把△BCD绕点B按逆时针方向旋转45°得到△BEG,此时EG交AD于点F.如果AD=1,那么AF=$\sqrt{2}-1$.
如图,连接正方形ABCD的对角线BD,把△BCD绕点B按逆时针方向旋转45°得到△BEG,此时EG交AD于点F.如果AD=1,那么AF=$\sqrt{2}-1$. 如图,在平行四边形ABCD中,点E、F分别在AD、BC上,且AE=CF.求证:BE∥DF.
如图,在平行四边形ABCD中,点E、F分别在AD、BC上,且AE=CF.求证:BE∥DF. 如图,水泥在传送带上移动的过程可以看做平移 变换.
如图,水泥在传送带上移动的过程可以看做平移 变换.