题目内容
8.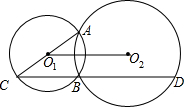 如图,⊙O1与⊙O2相交于A、B两点,连接AO1并延长交⊙O1于点C,连接CB并延长交⊙O2于点D,若O1O2=2,求CD的长.
如图,⊙O1与⊙O2相交于A、B两点,连接AO1并延长交⊙O1于点C,连接CB并延长交⊙O2于点D,若O1O2=2,求CD的长.
分析 如图,作辅助线;首先证明AD为⊙O2的直径,其次判断O1O2为△ACD的中位线,即可解决问题.
解答  解:如图,连接AB、AD;
解:如图,连接AB、AD;
∵AC为⊙O1的直径,
∴∠ABC=90°,∠ABD=180°-90°=90°,
∴AD为⊙O2的直径,
∴点O2在直径AD上;
∵O1A=O1C,O2A=O2D,
∴O1O2为△ACD的中位线,
∴CD=2O1O2=4.
点评 该题主要考查了相交两圆的性质、圆周角定理及其推论、三角形的中位线定理等几何知识点及其应用问题;解题的关键是作辅助线,构造三角形的中位线.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
20.若一个多边形每一个内角都是150°,则这个多边形的边数是( )
| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
18.化简(a+$\frac{1}{2}$)-2(3a-$\frac{2}{3}$)的结果是( )
| A. | -5a+$\frac{11}{6}$ | B. | -5a+$\frac{7}{6}$ | C. | -7a+$\frac{1}{3}$ | D. | -5a-$\frac{5}{6}$ |
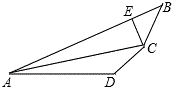 如图,AC平分∠BAD,CE⊥AB,且2AE=AB+AD,试探索∠ADC与∠ABC的关系.
如图,AC平分∠BAD,CE⊥AB,且2AE=AB+AD,试探索∠ADC与∠ABC的关系.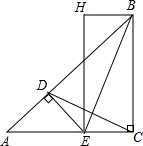 如图,△ABC和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,点D在AB上,点E在AC上,分别过B、E作AC、BC的平行线,两平行线交于点H.
如图,△ABC和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,点D在AB上,点E在AC上,分别过B、E作AC、BC的平行线,两平行线交于点H.