题目内容
19.在计算1$+\frac{1}{2}$$+\frac{1}{4}$$+\frac{1}{8}$+…$\frac{1}{{2}^{9}}$$+\frac{1}{{2}^{10}}$时,我们可设S=1+$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{{2}^{9}}$+$\frac{1}{{2}^{10}}$①,则2S=2+1+$\frac{1}{2}$+$\frac{1}{4}$+…+$\frac{1}{{2}^{9}}$②,由②-①,得S=2-$\frac{1}{{2}^{10}}$.(1)试用上述方法求$\frac{1}{2}$$+\frac{1}{4}$$+\frac{1}{8}$+…$+\frac{1}{{2}^{n}}$的值;
(2)试用上述方法求$\frac{1}{3}$$+\frac{1}{9}$$+\frac{1}{27}$+…$+\frac{1}{{3}^{n}}$的值.
分析 (1)设S=$\frac{1}{2}$$+\frac{1}{4}$$+\frac{1}{8}$+…$+\frac{1}{{2}^{n}}$,两边同乘2,再进一步把两式相减整理得出答案即可;
(2)设S=$\frac{1}{3}$$+\frac{1}{9}$$+\frac{1}{27}$+…$+\frac{1}{{3}^{n}}$,两边同乘3,再进一步把两式相减整理得出答案即可.
解答 解:(1)设S=$\frac{1}{2}$$+\frac{1}{4}$$+\frac{1}{8}$+…$+\frac{1}{{2}^{n}}$①,
则2s=1+$\frac{1}{2}$$+\frac{1}{4}$$+\frac{1}{8}$+…+$\frac{1}{{2}^{n-1}}$②,
由②-①,得S=1-$\frac{1}{{2}^{n}}$;
(2)设S=$\frac{1}{3}$$+\frac{1}{9}$$+\frac{1}{27}$+…$+\frac{1}{{3}^{n}}$①,
则3S=1+$\frac{1}{3}$$+\frac{1}{9}$$+\frac{1}{27}$+…+$\frac{1}{{3}^{n-1}}$②,
由②-①,得2S=1-$\frac{1}{{3}^{n}}$,
S=$\frac{1}{2}$-$\frac{1}{2×{3}^{n}}$.
点评 本题考查了有理数的乘方,读懂题目信息,理解求和的运算方法是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
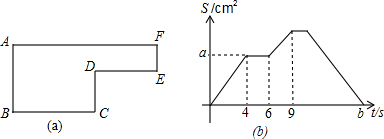
7.已知动点P以2厘米/秒的速度沿图(a)的边框 BCDEFA 的路径移动,相应的△ABP的面积S关于时间t的函数图象如图(b)所示.若 AB=6厘米,则下列答案正确的是( )

| A. | 图(a)中的BC长是4cm | B. | 图(b)中的a是12 | ||
| C. | 图(a)中的图形面积是60cm2 | D. | 图(b)中的b是19 |