题目内容
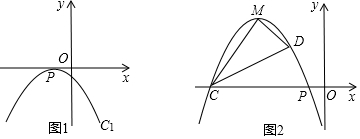
14. 如图,抛物线y=x2-3x+$\frac{5}{4}$与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E
如图,抛物线y=x2-3x+$\frac{5}{4}$与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E(1)求A、B的坐标;
(2)求直线BC的解析式;
(3)当线段DE的长度最大时,求点D的坐标.
分析 (1)通过解方程x2-3x+$\frac{5}{4}$=0可确定A点和B点坐标;
(2)先求出C点坐标,然后利用待定系数法求直线BC的解析式;
(3)设点D的横坐标为m,则纵坐标为(m,m2-3m+$\frac{5}{4}$),则E点的坐标为(m,-$\frac{1}{2}$m+$\frac{5}{4}$),则可利用m表示出DE,然后利用二次函数的性质求出m,从而可得到D点坐标.
解答 解:(1)当y=0时,x2-3x+$\frac{5}{4}$=0,解得x1=$\frac{1}{2}$,x2=$\frac{5}{2}$,
∴A($\frac{1}{2}$,0),B($\frac{5}{2}$,0);
(2)当x=0,则y=x2-3x+$\frac{5}{4}$=$\frac{5}{4}$,
∴C点坐标为(0,$\frac{5}{4}$),
设直线BC的解析式为y=kx+b,根据题意得$\left\{\begin{array}{l}{\frac{5}{2}k+b=0}\\{b=\frac{5}{4}}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=\frac{5}{4}}\end{array}\right.$,
∴直线BC的解析式为:y=-$\frac{1}{2}$x+$\frac{5}{4}$;
(3)设点D的横坐标为m,则纵坐标为(m,m2-3m+$\frac{5}{4}$),则E点的坐标为(m,-$\frac{1}{2}$m+$\frac{5}{4}$),
DE=-$\frac{1}{2}$m+$\frac{5}{4}$-(m2-3m+$\frac{5}{4}$)=-m2+$\frac{5}{2}$m,
∵DE=-(m-$\frac{5}{4}$)2+$\frac{25}{16}$
∴m=$\frac{5}{4}$时,DE的长最大,
∴D点的坐标为($\frac{5}{4}$,-$\frac{15}{16}$).
点评 本题考查了抛物线与x轴的交点:利用抛物线与x轴的交点坐标(x1,0),(x2,0)可设二次函数的交点式:y=a(x-x1)(x-x2)(a,b,c是常数,a≠0).也考查了二次函数的性质.

| 加数的个数n | 连续偶数的和S |
| 1 | 2=1×2 |
| 2 | 2+4=6=2×3 |
| 3 | 2+4+6=12=3×4 |
| 4 | 2+4+6+8=20=4×5 |
| 5 | 2+4+6+8+10=30=5×6 |
(1)如果n=8时,那么S的值为72;
(2)根据表中的规律猜想:用n的代数式表示S,则S=2+4+6+8+…+2n=n(n+1);
(3)利用上题的猜想结果,计算100+102+104+…+1010+1012的值(要有计算过程).
| 高度变化 | 记作 |
| 上升4.5km | +4.5km |
| 下降3.2km | -3.2km |
| 上升1.1km | +1.1km |
| 下降1.4km | -1.4km |
(2)如果飞机每上升或下降1千米需消耗2升燃油,那么这架飞机在这4个动作表演过程中,一共消耗了多少升燃油?
(3)如果飞机做特技表演时,有4个规定动作,起飞后高度变化如下:上升3.8千米,下降2.9千米,再上升1.6千米.若要使飞机最终比起飞点高出1千米,问第4个动作是上升还是下降,上升或下降多少千米?