题目内容
先化简,再求值:
÷(
-x+1),其中x是不等式组
的整数解.
| x2-2x+1 |
| x2-1 |
| x-1 |
| x+1 |
|
考点:分式的化简求值,一元一次不等式组的整数解
专题:
分析:先求出两个不等式的解集,再求其公共解,从而得到正整数x的值,再把被除式的分子分母分解因式,括号里面的通分并进行加法运算,然后把除法转化为乘法运算,约分,再求出使分式有意义的x的取值范围,然后代入进行计算即可得解.
解答:解:
,
解不等式①得,x≥-1,
解不等式②得,x≤2,
所以,不等式组的解集是-1≤x≤2,
∵x是整数,
∴x=0,±1,2,
÷(
-x+1),
=
÷
,
=
•
,
=-
,
要使分式有意义,则(x+1)(x-1)≠0,x≠0,
解得x≠±1,x≠0,
所以,x=2,
原式=-
.
|
解不等式①得,x≥-1,
解不等式②得,x≤2,
所以,不等式组的解集是-1≤x≤2,
∵x是整数,
∴x=0,±1,2,
| x2-2x+1 |
| x2-1 |
| x-1 |
| x+1 |
=
| (x-1)2 |
| (x+1)(x-1) |
| x-1-x2+1 |
| x+1 |
=
| x-1 |
| x+1 |
| x+1 |
| -x(x-1) |
=-
| 1 |
| x |
要使分式有意义,则(x+1)(x-1)≠0,x≠0,
解得x≠±1,x≠0,
所以,x=2,
原式=-
| 1 |
| 2 |
点评:本题考查了分式的化简求值,解一元一次不等式组,要注意先算括号里面的,分子、分母能因式分解的先因式分解;除法要统一为乘法运算,所取的数必须是使分式有意义.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 如图,以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点D恰好为BC的中点,过点D作⊙O的切线交AC边于点E.
如图,以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点D恰好为BC的中点,过点D作⊙O的切线交AC边于点E.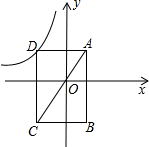 如图,矩形ABCD对角线AC经过原点O,B点坐标为(1,-3),若反比例函数
如图,矩形ABCD对角线AC经过原点O,B点坐标为(1,-3),若反比例函数 如图,△AOB与△A′OB′是位似图形,点O是位似中心,若2OA=OA′,S△AOB=8,则S△A′OB′=
如图,△AOB与△A′OB′是位似图形,点O是位似中心,若2OA=OA′,S△AOB=8,则S△A′OB′=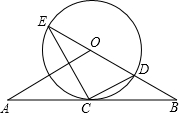 如图,直线AB经过⊙0上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,D,连接EC,CD.
如图,直线AB经过⊙0上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,D,连接EC,CD.