题目内容
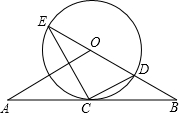 如图,直线AB经过⊙0上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,D,连接EC,CD.
如图,直线AB经过⊙0上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,D,连接EC,CD.(1)求证:BC2=BD•BE;
(2)若tan∠CED=
| 1 |
| 2 |
考点:切线的判定,相似三角形的判定与性质
专题:
分析:(1)如图,连接OC.构建相似三角形△BCD∽△BEC,根据该相似三角形的对应边成比例得到
=
,则BC2=BD•BE;
(2)利用正切三角函数的定义、(1)中的相似三角形的对应边成比例求得
=
=
.设BD=x(x>0).BC=2x.又BC2=BD•BE,则易求x=2,所以根据图中相关线段间的和差关系来求OA的长度.
| BC |
| BE |
| BD |
| BC |
(2)利用正切三角函数的定义、(1)中的相似三角形的对应边成比例求得
| BD |
| BC |
| CD |
| EC |
| 1 |
| 2 |
解答: (1)证明:如图,连接OC.
(1)证明:如图,连接OC.
∵OA=OB,CA=CB,
∴OC⊥AB,
∴OC是⊙O的切线.
∵ED是直径,
∴∠ECD=90°.
又∵∠BCD+∠OCD=90°,∠OCD=∠ODC,
∴∠BCD=∠E.
∵∠CBD=∠EBC,
∴△BCD∽△BEC,
∴
=
,
∴BC2=BD•BE;
(2)∵tan∠CED=
,
∴
=
.
由(1)知,△BCD∽△BEC,
∴
=
=
.
设BD=x(x>0),则BC=2x.又BC2=BD•BE,
∴(2x)2=x(x+6),
解得x=0(不合题意,舍去),或x=2.
∴BD=2,
∴OA=OB=BD+OD=3+2=5,即OA的长度是5.
 (1)证明:如图,连接OC.
(1)证明:如图,连接OC.∵OA=OB,CA=CB,
∴OC⊥AB,
∴OC是⊙O的切线.
∵ED是直径,
∴∠ECD=90°.
又∵∠BCD+∠OCD=90°,∠OCD=∠ODC,
∴∠BCD=∠E.
∵∠CBD=∠EBC,
∴△BCD∽△BEC,
∴
| BC |
| BE |
| BD |
| BC |
∴BC2=BD•BE;
(2)∵tan∠CED=
| 1 |
| 2 |
∴
| CD |
| EC |
| 1 |
| 2 |
由(1)知,△BCD∽△BEC,
∴
| BD |
| BC |
| CD |
| EC |
| 1 |
| 2 |
设BD=x(x>0),则BC=2x.又BC2=BD•BE,
∴(2x)2=x(x+6),
解得x=0(不合题意,舍去),或x=2.
∴BD=2,
∴OA=OB=BD+OD=3+2=5,即OA的长度是5.
点评:本题考查了切线的判定,相似三角形的判定与性质.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
宁波市是国家优秀旅游城市,吸引了众多的海内外游客.据宁波市2012年国民经济和社会发展统计公报显示,全年旅游总收入达862.8亿元.将862.8亿元用科学记数法可表示为( )
| A、86.28×109元 |
| B、86.28×1010元 |
| C、8.628×1010元 |
| D、8.628×1011元 |
甲、乙两个学习小组各有4名同学,在某次测验中,他们的得分情况如下表所示:
设两组同学得分的平均数依次为
甲,
乙,得分的方差依次为
,
,则下列关系中完全正确的是( )
| 组员1 | 组员2 | 组员3 | 组员4 | |
| 甲 | 88 | 95 | 97 | 100 |
| 乙 | 90 | 94 | 97 | 99 |
. |
| x |
. |
| x |
| S | 2 甲 |
| S | 2 乙 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
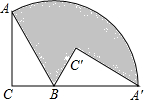 将直角△ABC绕顶点B旋转至如图位置,其中∠C=90°,AB=4,BC=2,点C、B、A在同一直线上,则阴影部分的面积是
将直角△ABC绕顶点B旋转至如图位置,其中∠C=90°,AB=4,BC=2,点C、B、A在同一直线上,则阴影部分的面积是 如图,抛物线y=ax2-4x+c的图象与x轴交于A(-3,0)、B(5,0)两点,则a的值为
如图,抛物线y=ax2-4x+c的图象与x轴交于A(-3,0)、B(5,0)两点,则a的值为 如图,⊙O与AC相切于点A,BC过圆心O,圆周角∠B=25°,则∠C的度数为
如图,⊙O与AC相切于点A,BC过圆心O,圆周角∠B=25°,则∠C的度数为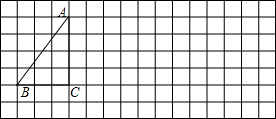 将下列方格纸中的△ABC向右平移10格,再向上平移2格,得到△A1B1C1.
将下列方格纸中的△ABC向右平移10格,再向上平移2格,得到△A1B1C1.