题目内容
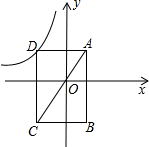 如图,矩形ABCD对角线AC经过原点O,B点坐标为(1,-3),若反比例函数y=
如图,矩形ABCD对角线AC经过原点O,B点坐标为(1,-3),若反比例函数y=| k |
| x |
考点:反比例函数图象上点的坐标特征
专题:
分析:先求出△ADC∽△AEO,再根据k的几何意义求出k值即可.
解答: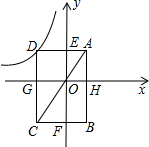 解:设D的坐标为(m,n),又B(1,-3),
解:设D的坐标为(m,n),又B(1,-3),
∴BH=CG=3,BF=1,DE=OG=FC=-m,AH=DG=n,
∴CD=DG+CG=3+n,AD=AE+DE=1-m,
∵∠ADC=∠AEO=90°,∠DAC=∠DAC,
∴△ADC∽△AEO,
∴
=
,即
=
,
整理得:3+n=n-mn,即mn=-3,
则k=-3.
故答案为:-3.
 解:设D的坐标为(m,n),又B(1,-3),
解:设D的坐标为(m,n),又B(1,-3),∴BH=CG=3,BF=1,DE=OG=FC=-m,AH=DG=n,
∴CD=DG+CG=3+n,AD=AE+DE=1-m,
∵∠ADC=∠AEO=90°,∠DAC=∠DAC,
∴△ADC∽△AEO,
∴
| AE |
| AD |
| EO |
| DC |
| 1 |
| 1-m |
| n |
| 3+n |
整理得:3+n=n-mn,即mn=-3,
则k=-3.
故答案为:-3.
点评:此题主要考查了相似三角形的判定与性质以及反比例函数图象上点的坐标性质,得出△ADC∽△AEO是解题关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
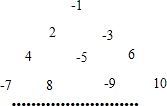 将一组整数按如图所示的规律排列下去.若有序数对(n,m)表示第n排,从左到右第m个数,如(4,2)表示的数为8,则(7,4)表示的数是( )
将一组整数按如图所示的规律排列下去.若有序数对(n,m)表示第n排,从左到右第m个数,如(4,2)表示的数为8,则(7,4)表示的数是( )| A、32 | B、24 | C、-25 | D、26 |
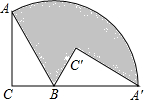 将直角△ABC绕顶点B旋转至如图位置,其中∠C=90°,AB=4,BC=2,点C、B、A在同一直线上,则阴影部分的面积是
将直角△ABC绕顶点B旋转至如图位置,其中∠C=90°,AB=4,BC=2,点C、B、A在同一直线上,则阴影部分的面积是
 如图,至少找出下列几何体的4个共同点.
如图,至少找出下列几何体的4个共同点. 如图,抛物线y=ax2-4x+c的图象与x轴交于A(-3,0)、B(5,0)两点,则a的值为
如图,抛物线y=ax2-4x+c的图象与x轴交于A(-3,0)、B(5,0)两点,则a的值为