题目内容
16．
如图，在△ABC中，∠C=90°，∠ABC=60°，若CD=2，AB=6，则S△ABD=$\frac{9\sqrt{3}}{2}$-3．
分析 先利用含30°的直角三角形的性质求出BC，AC进而得出AD，最后用三角形的面积公式即可得出结论．
解答 解：在Rt△ABC中，∠ABC=60°，
∴∠A=30°，
∵AB=6，
∴BC=$\frac{1}{2}$AB=3，AC=$\sqrt{3}$BC=3$\sqrt{3}$，
∵CD=2，
∴AD=AC-CD=3$\sqrt{3}$-2，
∴S△ABD=$\frac{1}{2}$AD•BC=$\frac{1}{2}$×（3$\sqrt{3}$-2）×3=$\frac{9\sqrt{3}}{2}$-3，
故答案为：$\frac{9\sqrt{3}}{2}$-3．
点评 此题是解直角三角形，主要考查了含30°的直角三角形的性质，三角形的面积公式，求出AD是解本题的关键．
练习册系列答案
相关题目
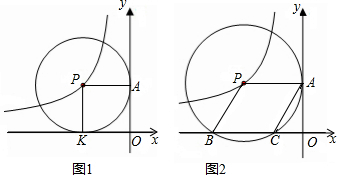
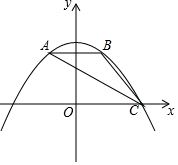如图，抛物线y=ax2+$\frac{9}{4}$经过△ABC的三个顶点，点A坐标为（-1，2），点B是点A关于y轴的对称点，点C在x轴的正半轴上．
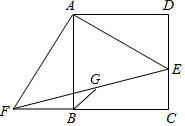E为正方形ABCD的边CD上一点，将△ADE绕A点顺时针旋转90°，得△ABF，G为EF中点．下列结论：①G在△ABF的外接圆上；②EC=$\sqrt{2}$BG；③B，G，D三点在同一条直线上；④若S四边形BGEC=$\frac{1}{4}$S正方形ABCD，那么E为DC的黄金分割点．正确的是（ ）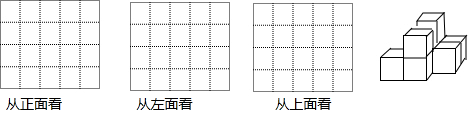
已知抛物线y=-x2+bx+3交x轴负、正半轴于A、B两点，交y轴与点C，且tan∠ACO=$\frac{1}{3}$，△ABC的外接圆的圆心为M．
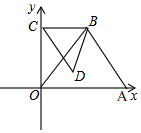如图，直角坐标系中，O为原点，A（6，0），在等腰三角形ABO中，OB=BA=5，点B在第一象限，C（0，k）为y轴正半轴上一动点，作以∠CBD为顶角的等腰三角形CBD，且∠CBD=∠OBA，连结AD．
如图，直线a经过点A（0，1）且垂直于y轴，直线b经过点B（2，0）且垂直于x轴，反比例函数y=$\frac{k}{x}$（k≠0）在第一象限内的图象与直线a，b分别交于点E、D．