题目内容
 在平面直角坐标系中放置了一个边长为
在平面直角坐标系中放置了一个边长为| 5 |
考点:全等三角形的判定与性质,坐标与图形性质
专题:
分析:如图,作辅助线;证明△OBC≌△ECD,得到DE=OC,CE=OB;求出OC、OB的长度,即可解决问题.
解答: 解:如图,过点D作DE⊥x轴于点E;
解:如图,过点D作DE⊥x轴于点E;
∵四边形ABCD为正方形,
∴∠BCD=90°,而∠BOC=90°,
∴∠OBC+∠OCB=∠OCB+∠DCE,
∴∠OBC=∠DCE;在△OBC与△ECD中,
,
∴△OBC≌△ECD(AAS),
∴DE=OC,CE=OB;
由题意得:BC2=OB2+OC2,而OB=2,BC=
,
∴OC=1,DE=1,CE=2,
∴点D的坐标为(3,1).
故答案为(3,1).
 解:如图,过点D作DE⊥x轴于点E;
解:如图,过点D作DE⊥x轴于点E;∵四边形ABCD为正方形,
∴∠BCD=90°,而∠BOC=90°,
∴∠OBC+∠OCB=∠OCB+∠DCE,
∴∠OBC=∠DCE;在△OBC与△ECD中,
|
∴△OBC≌△ECD(AAS),
∴DE=OC,CE=OB;
由题意得:BC2=OB2+OC2,而OB=2,BC=
| 5 |
∴OC=1,DE=1,CE=2,
∴点D的坐标为(3,1).
故答案为(3,1).
点评:该题以平面直角坐标系为载体,以坐标与图形的关系、全等三角形的判定及其性质的应用为考查的核心构造而成;对综合的分析问题解决问题的能力提除了一定的要求.

练习册系列答案
相关题目
若x-y≠0,2x-3y=0,则分式
的值是( )
| 10x-11y |
| x-y |
| A、-12 | ||
| B、0 | ||
| C、8 | ||
D、8
|
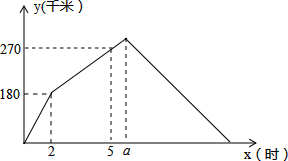 甲、乙两车都从同一地点沿同一路线驶向同一目的地,甲车先行,一段时间后,乙车开始行驶,甲车到达目的地后,乙车走完了全程的
甲、乙两车都从同一地点沿同一路线驶向同一目的地,甲车先行,一段时间后,乙车开始行驶,甲车到达目的地后,乙车走完了全程的