题目内容
 如图,已知AB∥DC,AD∥BC,AM=CN,图中全等三角形有
如图,已知AB∥DC,AD∥BC,AM=CN,图中全等三角形有考点:全等三角形的判定
专题:
分析:根据AD∥BC可得∠MAO=∠NCO,然后证明△AMO≌△CNO,可得AO=CO再证明△AOD≌△COB可得BO=DO,∠MDO=∠NBO,进而可证明△MOD≌△NOB,再证明△ADB≌△CBD,△ABO≌△CDO,△ABC≌△CDA.
解答:解:∵AD∥BC,
∴∠MAO=∠NCO,
在△AMO和△CNO中,
,
∴△AMO≌△CNO(AAS),
∴AO=CO,
在△AOD和△COB中,
,
∴△AOD≌△COB(ASA),
∴BO=DO,∠MDO=∠NBO,
在△MOD和△NOB中,
,
∴△MOD≌△NOB(ASA),
∴MD=BN,
∴AD=BC,
在△ADB和△CBD中,
,
∴△ADB≌△CBD(SAS),
∴AB=CD,∠ABD=∠CDB,
在△ABO和△CDO中,
,
∴△ABO≌△CDO(AAS),
在△ABC和△CDA中,
,
∴△ABC≌△CDA(SSS).
共有6对全等三角形.
故答案为:6.
∴∠MAO=∠NCO,
在△AMO和△CNO中,
|
∴△AMO≌△CNO(AAS),

∴AO=CO,
在△AOD和△COB中,
|
∴△AOD≌△COB(ASA),
∴BO=DO,∠MDO=∠NBO,
在△MOD和△NOB中,
|
∴△MOD≌△NOB(ASA),
∴MD=BN,
∴AD=BC,
在△ADB和△CBD中,
|
∴△ADB≌△CBD(SAS),
∴AB=CD,∠ABD=∠CDB,
在△ABO和△CDO中,
|
∴△ABO≌△CDO(AAS),
在△ABC和△CDA中,
|
∴△ABC≌△CDA(SSS).
共有6对全等三角形.
故答案为:6.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
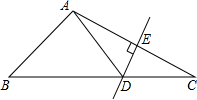 如图,在△ABC中,DE是AC的垂直平分线,AC=6cm,且△ABD的周长为13cm,则△ABC的周长为( )cm.
如图,在△ABC中,DE是AC的垂直平分线,AC=6cm,且△ABD的周长为13cm,则△ABC的周长为( )cm.| A、13 | B、19 | C、10 | D、16 |
 如图,已知∠AOC:∠BOC=4:5,且OE⊥CD,则∠AOE=
如图,已知∠AOC:∠BOC=4:5,且OE⊥CD,则∠AOE= 在平面直角坐标系中,四边形AOBC是菱形.若点A的坐标是(3,4),点C的坐标是
在平面直角坐标系中,四边形AOBC是菱形.若点A的坐标是(3,4),点C的坐标是