题目内容
 如图,在直角坐标系中,△ABC的各顶点坐标为A(-1,1),B(2,3),C(0,3).现以坐标原点为位似中心,作△A′B′C′,使△A′B′C′与△ABC的位似比为
如图,在直角坐标系中,△ABC的各顶点坐标为A(-1,1),B(2,3),C(0,3).现以坐标原点为位似中心,作△A′B′C′,使△A′B′C′与△ABC的位似比为| 2 |
| 3 |
考点:位似变换,坐标与图形性质
专题:
分析:位似是特殊的相似,若两个图形△ABC和△A′B′C′以原点为位似中心,相似比是k,△ABC上一点的坐标是(x,y),则在△A′B′C′中,它的对应点的坐标是(kx,ky)或(-kx,-ky).
解答:解:∵在△A′B′C′中,它的对应点的坐标是(kx,ky)或(-kx,-ky)
∴A'的坐标为:(-
,
)或(
,-
).
故答案为:(-
,
)或(
,-
).
∴A'的坐标为:(-
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
故答案为:(-
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
点评:此题主要考查了位似变换,正确理解位似与相似的关系,记忆关于原点位似的两个图形对应点坐标之间的关系是解题的关键.

练习册系列答案
相关题目
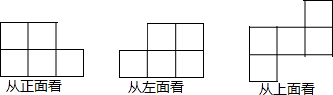 如图是由几个完全相同的小正方形搭成的几何体从正面、左面、上面看到的形状图,则搭成这样的几何体所用的小正方形的个数最少是( )
如图是由几个完全相同的小正方形搭成的几何体从正面、左面、上面看到的形状图,则搭成这样的几何体所用的小正方形的个数最少是( )| A、8个 | B、7个 | C、6个 | D、5个 |
 如图,已知圆心角∠BOC=76°,则圆周角∠BAC的度数是( )
如图,已知圆心角∠BOC=76°,则圆周角∠BAC的度数是( )| A、152° | B、76° |
| C、38° | D、36° |
计算:(-73)+9.1-(-7)+(-9),正确的结果是( )
| A、-79.9 | B、61.9 |
| C、-65.9 | D、65.9 |
二次函数y=-(x-3)2+1的最大值为( )
| A、1 | B、-1 | C、3 | D、-3 |
 如图,在平面直角坐标系中,⊙P的圆心坐标是(4,a)(a>4),半径为4,函数y=x的图象被⊙P截得的弦AB的长为2
如图,在平面直角坐标系中,⊙P的圆心坐标是(4,a)(a>4),半径为4,函数y=x的图象被⊙P截得的弦AB的长为2 某学校开展数学竞赛,八(1)、八(2)班根据初赛成绩各选出5名选手参加复赛,两个班的5名选手的复赛成绩如图所示.根据图示回答:一班复赛成绩的中位数是
某学校开展数学竞赛,八(1)、八(2)班根据初赛成绩各选出5名选手参加复赛,两个班的5名选手的复赛成绩如图所示.根据图示回答:一班复赛成绩的中位数是