题目内容
15.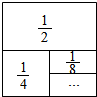 我国著名数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事非.”如图,在一个边长为1的正方形纸版上,依次贴上面积为$\frac{1}{2}$,$\frac{1}{4}$,$\frac{1}{8}$,…,$\frac{1}{{2}^{n}}$的矩形彩色纸片(n为大于1的整数).请你用“数形结合”的思想,依数形变化的规律,计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{{2}^{n}}$=1-$\frac{1}{{2}^{n}}$.
我国著名数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事非.”如图,在一个边长为1的正方形纸版上,依次贴上面积为$\frac{1}{2}$,$\frac{1}{4}$,$\frac{1}{8}$,…,$\frac{1}{{2}^{n}}$的矩形彩色纸片(n为大于1的整数).请你用“数形结合”的思想,依数形变化的规律,计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{{2}^{n}}$=1-$\frac{1}{{2}^{n}}$.
分析 由题意可知正方形的总面积为1,然后,通过观察未贴部分,来确定已贴部分总面积:贴$\frac{1}{2}$,余$\frac{1}{2}$,再贴$\frac{1}{2}$,余$\frac{1}{4}$,则$\frac{1}{2}$+$\frac{1}{4}$=1-$\frac{1}{4}$,再贴$\frac{1}{8}$,余$\frac{1}{8}$,则$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$=1-$\frac{1}{8}$,所以,$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{{2}^{n}}$=1-$\frac{1}{{2}^{n}}$.
解答 解:∵正方形的边长为1,
∴正方形的面积为1,
∵正方形减去未贴部分的面积既是已帖部分的面积,
$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{{2}^{n}}$=1-$\frac{1}{{2}^{n}}$,
故答案为:1-$\frac{1}{{2}^{n}}$.
点评 本题主要考查通过分析总结归纳规律,关键在于用“数形结合”的思想,分析出余下部分的面积,即可推出已帖部分的面积.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
6.一个立方体的棱长之和是24厘米,它的表面积是( )平方厘米.
| A. | 96 | B. | 48 | C. | 24 | D. | 12 |
3.把一个棱长是6厘米的立方体,切成棱长是3厘米的小立方体,表面积增加了( )
| A. | 36平方厘米 | B. | 108平方厘米 | C. | 216平方厘米 | D. | 432平方厘米 |
20.老师有事要电话通知全班10名同学,如果每分钟打电话通知1人,那么最快要( )可通知完.
| A. | 4分钟 | B. | 10分钟 | C. | 7分钟 |
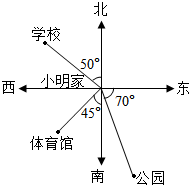 (1)学校在小明家的北偏西50° 方向上.
(1)学校在小明家的北偏西50° 方向上.