题目内容
20.求1+2+22+23+…+22012的值,可令S=1+2+22+23+…+22012,则2S=2+22+23+24+…+22013,因此2S-S=22013-1.仿照以上推理,计算出1+5+52+53+…+52012的值为( )| A. | 52012-1 | B. | 52013-1 | C. | $\frac{{5}^{2013}-1}{4}$ | D. | $\frac{{5}^{2012}-1}{4}$ |
分析 观察题目中所给的推理方法:可以发现,当乘方的底数为2的时候,把原式乘上2,再与原式相减即可得出答案;因此当乘方中底数为5时,把原式乘上5,得到与原式类似的式子,再减去原式即可得到答案.据此解决.
解答 解:设S=1+5+52+53+…+52012,
则5S=5+52+53+54+…+52013,
所以5S-S=(5+52+53+54+…+52013)-(1+5+52+53+…+52012)
=5+52+53+54+…+52013-1-5-52-53-…-52012
=52013-1,
即4S=52013-1
所以S=$\frac{{5}^{2013}-1}{4}$;
故选:C.
点评 解决本题的关键是观察题干中的推理过程,找到规律,然后应用规律解决问题.

练习册系列答案
相关题目
 妈妈的茶杯这样放在桌子上(如图).
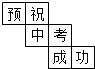
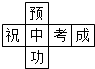
妈妈的茶杯这样放在桌子上(如图). 小亮为今年参加中考的好友小杰制作了一个正方体礼品盒(如图),六个面上各有一个字,连起来就是“预祝中考成功”,其中“预”的对面是“中”,“成”的对面是“功”,则它的平面展开图可能是( )
小亮为今年参加中考的好友小杰制作了一个正方体礼品盒(如图),六个面上各有一个字,连起来就是“预祝中考成功”,其中“预”的对面是“中”,“成”的对面是“功”,则它的平面展开图可能是( )