题目内容

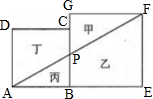
如图，有边长分别是15分米和20分米的两个正方形，一条直线把这两个相连的正方形分成甲、乙、丙、丁四部分．甲三角形的面积比丙三角形的面积大多少平方分米？

分析：如图，根据图意，PB∥EF，所以△ABP∽△AEF，所以AB：AE=BP：EF，即15：（15+20）=BP：20，因此，BP=

15×20

15+20

300

（分米），PG=20-

（分米），根据已知条件可分别求出甲三角形和丙三角形的面积，进而求出甲三角形的面积比丙三角形的面积大多少平方分米．

解答：解：如图，

甲三角形的面积是：

×20×

=114

（平方分米），
丙三角形的面积是：

×15×

=64

（平方分类），
114

-64

=50（平方分米）；
故答案为：50平方分米．

点评：解答此题的关键是根据相似三角形求出直线把大正方形分成的两部分的长．用小学知识解答有一定难度．

练习册系列答案

初中满分冲刺卷系列答案

相关题目

看图计算．

（1）如图1，已知正方形的面积为64平方厘米，求阴影部分的面积．
（2）如图2，在直角梯形ABCD中，AB=8，BC=14厘米，AD=10厘米，△DCF的面积是梯形ABCD面积的 $数学公式$ ，△ADE的面积是梯形ABCD面积的 $数学公式$ ，求阴影部分面积．
（3）如图3，正方形ABCD的边长是6厘米，E、F分别是AB、BC的中点，求阴影部分的面积？
（4）如图4，有一个底面周长为6.28厘米的圆柱体，被斜着截去一段，现在的体积是多少？

阅读以下两则材料，并完成后面的4个问题．
材料一、如果一个正数x的平方等于a，即x²=a（a＞0），那么x叫作a的算术平方根，记作x= $数学公式$ ．例如，因为2²=4，所以2是4的算术平方根，记作 $数学公式$ =2
材料二、直角三角形两直角边的平方和等于斜边的平方，例如，如图所示，直角三角形ABC中，如果∠ACB-90°，AC=3，BC=4，因为3²+4²=5²，所以斜边AB=5．
问题：
（1）9的算术平方根是，10的算术平方根是；
（2）某直角三角形的两条直角边分别是5，12，则斜边长是；
（3）某直角三角形有两条边的长分别是1与2，则第三条边的长是；
（4）请你计算上述第（3）中直角三角形斜边上的高是__．