题目内容
看图计算.

(1)如图1,已知正方形的面积为64平方厘米,求阴影部分的面积.
(2)如图2,在直角梯形ABCD中,AB=8,BC=14厘米,AD=10厘米,△DCF的面积是梯形ABCD面积的
,△ADE的面积是梯形ABCD面积的
,求阴影部分面积.
(3)如图3,正方形ABCD的边长是6厘米,E、F分别是AB、BC的中点,求阴影部分的面积?
(4)如图4,有一个底面周长为6.28厘米的圆柱体,被斜着截去一段,现在的体积是多少?

(1)如图1,已知正方形的面积为64平方厘米,求阴影部分的面积.
(2)如图2,在直角梯形ABCD中,AB=8,BC=14厘米,AD=10厘米,△DCF的面积是梯形ABCD面积的
| 1 |
| 4 |
| 3 |
| 8 |
(3)如图3,正方形ABCD的边长是6厘米,E、F分别是AB、BC的中点,求阴影部分的面积?
(4)如图4,有一个底面周长为6.28厘米的圆柱体,被斜着截去一段,现在的体积是多少?
分析:(1)因为8×8=64,所以正方形的边长是8厘米,那么正方形内最大的圆的直径就是8厘米,那么阴影部分的面积就是正方形的面积减去3个空白处的面积,再减去半径为8÷2=4厘米的
圆的面积;
(2)阴影部分的面积=梯形的面积-△DCF的面积-△ADE的面积-△BEF的面积;
根据题干不难求出这个梯形ABCD的面积,从而求出:△DCF的面积和△ADE的面积;利用三角形的面积公式分别求出BE、BF的长度,从而求出△BEF的面积即可解答.
(3)如图,仔细一看你会发现把把大正方形的四个角的小三角形拼起来得到5个面积相等的小正方形,每个小正方形的面积都是这个大正方形的面积的
,则阴影部分的面积就是其中一个小正方形的面积;
(4)先利用圆柱的底面周长求出它的底面半径,这个图形的体积是高为5厘米的圆柱的体积与高为6-5=1厘米的圆柱的一半的体积之和.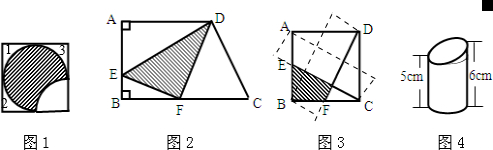
| 1 |
| 4 |
(2)阴影部分的面积=梯形的面积-△DCF的面积-△ADE的面积-△BEF的面积;
根据题干不难求出这个梯形ABCD的面积,从而求出:△DCF的面积和△ADE的面积;利用三角形的面积公式分别求出BE、BF的长度,从而求出△BEF的面积即可解答.
(3)如图,仔细一看你会发现把把大正方形的四个角的小三角形拼起来得到5个面积相等的小正方形,每个小正方形的面积都是这个大正方形的面积的
| 1 |
| 5 |
(4)先利用圆柱的底面周长求出它的底面半径,这个图形的体积是高为5厘米的圆柱的体积与高为6-5=1厘米的圆柱的一半的体积之和.

解答:解:(1)已知正方形的面积是64平方厘米,因为8×8=64,
所以正方形的边长是8厘米,则阴影部分圆的半径是8÷2=4(厘米),空白处
圆的半径是4厘米,
左边3个空白处的面积分别是:
(64-3.14×42)÷4,
=(64-3.14×16)÷4,
=(64-50.24)÷4,
=13.76÷4,
=3.44(平方厘米),
所以阴影部分的面积是:
64-3.44×3-
×3.14×42,
=64-10.32-12.56,
=41.12(平方厘米),
答:阴影部分的面积是41.12平方厘米.
(2)梯形的面积是:(10+14)×8÷2,
=24×4,
=96(平方厘米),
则△DCF的面积是:96×
=24(平方厘米),
△ADE的面积是:96×
=36(平方厘米),
所以AE的长度是:36×2÷10=7.2(厘米),则BE=8-7.2=0.8(厘米),
则FC的长度是:24×2÷8=6(厘米),所以BF=14-6=8(厘米),
△BEF的面积是:0.8×8÷2=3.2(平方厘米),
则阴影部分的面积是:96-24-36-3.2=32.8(平方厘米),
答:阴影部分的面积是32.8平方厘米.
(3)6×6÷5,
=36÷5,
=7.2(平方厘米),
答:阴影部分的面积是7.2平方厘米.
(4)底面半径为:
6.28÷3.14÷2=1(厘米),
3.14×12×5+3.14×12×(6-5)÷2,
=15.7+3.14×1÷2,
=15.7+1.57,
=17.27(立方厘米);
答:现在的体积是17.27立方厘米.
所以正方形的边长是8厘米,则阴影部分圆的半径是8÷2=4(厘米),空白处
| 1 |
| 4 |
左边3个空白处的面积分别是:
(64-3.14×42)÷4,
=(64-3.14×16)÷4,
=(64-50.24)÷4,
=13.76÷4,
=3.44(平方厘米),
所以阴影部分的面积是:
64-3.44×3-
| 1 |
| 4 |
=64-10.32-12.56,
=41.12(平方厘米),
答:阴影部分的面积是41.12平方厘米.
(2)梯形的面积是:(10+14)×8÷2,
=24×4,
=96(平方厘米),
则△DCF的面积是:96×
| 1 |
| 4 |
△ADE的面积是:96×
| 3 |
| 8 |
所以AE的长度是:36×2÷10=7.2(厘米),则BE=8-7.2=0.8(厘米),
则FC的长度是:24×2÷8=6(厘米),所以BF=14-6=8(厘米),
△BEF的面积是:0.8×8÷2=3.2(平方厘米),
则阴影部分的面积是:96-24-36-3.2=32.8(平方厘米),
答:阴影部分的面积是32.8平方厘米.
(3)6×6÷5,
=36÷5,
=7.2(平方厘米),
答:阴影部分的面积是7.2平方厘米.
(4)底面半径为:
6.28÷3.14÷2=1(厘米),
3.14×12×5+3.14×12×(6-5)÷2,
=15.7+3.14×1÷2,
=15.7+1.57,
=17.27(立方厘米);
答:现在的体积是17.27立方厘米.
点评:此题考查了组合图形的面积的计算方法的灵活应用,一般都是把组合图形的面积转移到规则图形中利用面积公式即可解答.

练习册系列答案
相关题目
 (2012?济南模拟)看图计算.
(2012?济南模拟)看图计算.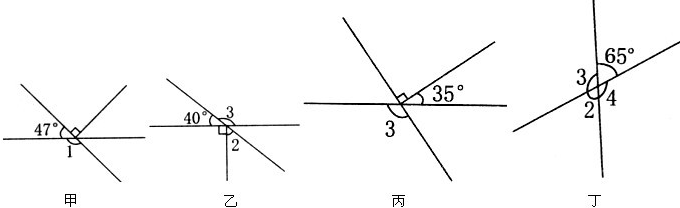

 ,△ADE的面积是梯形ABCD面积的
,△ADE的面积是梯形ABCD面积的 ,求阴影部分面积.
,求阴影部分面积.