题目内容
已知:
=
-
=
-
=
-
利用提供的信息计算下题(写出主要计算过程)
+
+
+
+
+
+
+
=
| 1 |
| 1×2 |
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 4×5 |
| 1 |
| 5×6 |
| 1 |
| 6×7 |
| 1 |
| 7×8 |
| 1 |
| 8×9 |
分析:根据已知:
=
-
=
-
=
-
得出规律
=
-
,即可得出:
=
-
,
=
-
,
=
-
,
=
-
,当把这些等式的左边相加时,就等于右边的两个分数相加,前一个分数的后一项和后面分数的前一项刚好抵消,因此得解.
| 1 |
| 1×2 |
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n×(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 4×5 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6×7 |
| 1 |
| 6 |
| 1 |
| 7 |
| 1 |
| 7×8 |
| 1 |
| 7 |
| 1 |
| 8 |
| 1 |
| 8×9 |
| 1 |
| 8 |
| 1 |
| 9 |
解答:解:
+
+
+
+
+
+
+
,
=(
-
)+(
-
)+(
-
)+(
-
)+(
-
)+(
-
)+(
-
)+(
-
),
=
-
,
=
.
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 4×5 |
| 1 |
| 5×6 |
| 1 |
| 6×7 |
| 1 |
| 7×8 |
| 1 |
| 8×9 |
=(
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 7 |
| 1 |
| 7 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 9 |
=
| 1 |
| 1 |
| 1 |
| 9 |
=
| 8 |
| 9 |
点评:灵活运用分数的拆项使复杂的计算简单化.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
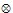 n=k(k为常数)时,(m+1)
n=k(k为常数)时,(m+1)