题目内容
规定:当m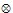 n=k(k为常数)时,(m+1)
n=k(k为常数)时,(m+1)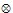 n=k-1,m
n=k-1,m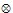 (n+1)=k+2.
(n+1)=k+2.
已知:1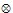 1=2,那么2010
1=2,那么2010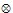 2011
2011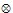 2012
2012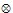 2013=
2013=
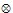 n=k(k为常数)时,(m+1)
n=k(k为常数)时,(m+1)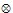 n=k-1,m
n=k-1,m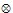 (n+1)=k+2.
(n+1)=k+2.已知:1
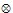 1=2,那么2010
1=2,那么2010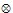 2011
2011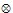 2012
2012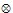 2013=
2013=2013
2013
.分析:当m增加1,运算结果就减少1,当m增加a时,运算结果k就减少a;当n增加1,运算结果k就增加2,当n增加b时,运用结果k就减少2b,由此求解.
解答:解:现在已知:1?1=2,即m=1,n=1,k=2,
2010?2011?2012?2013,
=(1+2009)?(1+2010)?2012?2013,
=(2010×2-2009)?2012?2013,
=2011?2012?2013,
=(1+2010)?(1+2011)?2013,
=(2011×2-2010)?2013,
=2012?2013,
=(1+2011)?(1+2012),
=2012×2-2011,
=2013;
故答案为:2013.
2010?2011?2012?2013,
=(1+2009)?(1+2010)?2012?2013,
=(2010×2-2009)?2012?2013,
=2011?2012?2013,
=(1+2010)?(1+2011)?2013,
=(2011×2-2010)?2013,
=2012?2013,
=(1+2011)?(1+2012),
=2012×2-2011,
=2013;
故答案为:2013.
点评:根据已知条件,找出?前后两个数的变化对运算结果的影响,进而解决问题,属于四则混合运算的拓展.

练习册系列答案
相关题目