题目内容
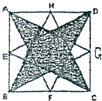 如图,E,F,G,H是边长为2的正方形ABCD各边的中点,则图中阴影部分的面积等于
如图,E,F,G,H是边长为2的正方形ABCD各边的中点,则图中阴影部分的面积等于2
2
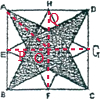
.分析:如下图,连接EG、HF、OA,则正方形ABCD被分成了4个相等的小正方形,阴影部分的面积被分成了相等的4份;在正方形AEOH中,E是AB的中点,G是CD的中点,得出P是EO的中点,由此得出三角形AOP的面积是三角形AEO的面积的一半,同理三角形AQO的面积是三角形AHO的面积的一半,进而得出阴影APOQ的面积是小正方形AEOH的面积的一半,因此图中阴影部分的面积是大正方形面积的一半.

解答:解:根据题干分析可得:2×2×
=2,
答:阴影部分的面积是2.
故答案为:2.
| 1 |
| 2 |
答:阴影部分的面积是2.
故答案为:2.
点评:解答此题的关键是,正确添加辅助线,利用等底同高的性质,判断三角形之间的关系,进而得出阴影部分与正方形的关系,由此得出答案.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,正方体的边长是10厘米,E、F、G、H分别是正方体底面各边的中点,这四点依次与正方体的顶点K连接,求阴影部分的体积(保留两位小数).
如图,正方体的边长是10厘米,E、F、G、H分别是正方体底面各边的中点,这四点依次与正方体的顶点K连接,求阴影部分的体积(保留两位小数). 如图所示,E,F,G,H分别是四边形各边中点,EG与FH交于点O,s1,s2,s3及 S4分别表示四个小四边形的面积.试比较 s1+s3与 s2+s4的大小?
如图所示,E,F,G,H分别是四边形各边中点,EG与FH交于点O,s1,s2,s3及 S4分别表示四个小四边形的面积.试比较 s1+s3与 s2+s4的大小?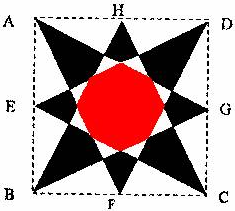 如图中,ABCD是边长为1的正方形,A,E,F,G,H分别是四条边AB,BC,CD,DA的中点,计算图中红色八边形的面积.
如图中,ABCD是边长为1的正方形,A,E,F,G,H分别是四条边AB,BC,CD,DA的中点,计算图中红色八边形的面积. 如图,E,F,G,H是边长为2的正方形ABCD各边的中点,则图中阴影部分的面积等于________.
如图,E,F,G,H是边长为2的正方形ABCD各边的中点,则图中阴影部分的面积等于________.