题目内容
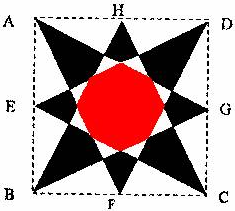 如图中,ABCD是边长为1的正方形,A,E,F,G,H分别是四条边AB,BC,CD,DA的中点,计算图中红色八边形的面积.
如图中,ABCD是边长为1的正方形,A,E,F,G,H分别是四条边AB,BC,CD,DA的中点,计算图中红色八边形的面积.分析:方法一:先求出小正方形中每个空白部分的面积,进而用小正方形的面积-空白部分的面积,即可得解;
方法二:将红色部分等分成8份,求出一部分的面积,问题即可得解.
方法二:将红色部分等分成8份,求出一部分的面积,问题即可得解.
解答:解:方法一:
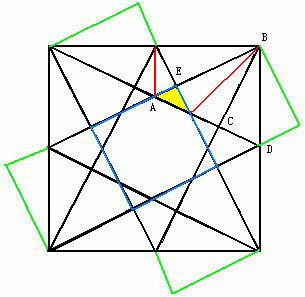
如图,易知蓝边正方形面积为
,△ABD面积为
,△BCD面积为
,
所以△ABC面积为
-
=
,可证AE:EB=1:4,
黄色三角形面积为△ABC的
,等于
,由此可得,所求八边形的面积是:
-4×
=
.
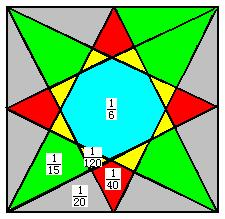
至此,我们对各部分的面积都已计算出来,如下图所示.
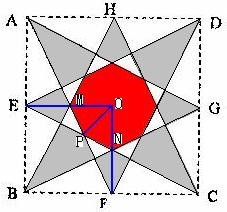
方法二:
设O为正方形中心(对角线交点),连接OE、OF,分别与AF、BG交于M、N,
设AF与EC的交点为P,连接OP,△MOF的面积为正方形面积的
,N为OF中点,
△OPN面积等于△FPN面积,又△OPN面积与△OPM面积相等,
所以△OPN面积为△MOF面积的
,为正方形面积的
,
八边形面积等于△OPM面积的8倍,为正方形面积的
.
如图,易知蓝边正方形面积为
| 1 |
| 5 |
| 1 |
| 8 |
| 1 |
| 20 |
所以△ABC面积为
| 1 |
| 8 |
| 1 |
| 20 |
| 3 |
| 40 |
黄色三角形面积为△ABC的
| 1 |
| 9 |
| 1 |
| 120 |
| 1 |
| 5 |
| 1 |
| 120 |
| 1 |
| 6 |
至此,我们对各部分的面积都已计算出来,如下图所示.


方法二:
设O为正方形中心(对角线交点),连接OE、OF,分别与AF、BG交于M、N,
设AF与EC的交点为P,连接OP,△MOF的面积为正方形面积的
| 1 |
| 16 |
△OPN面积等于△FPN面积,又△OPN面积与△OPM面积相等,
所以△OPN面积为△MOF面积的
| 1 |
| 3 |
| 1 |
| 48 |
八边形面积等于△OPM面积的8倍,为正方形面积的
| 1 |
| 6 |

点评:解答此题的关键是:弄清楚红色部分的面积可以由哪些图形的面积和或差求解,从而解决问题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 如图,正方形ABCD的边长为12,P是边AB上的任意一点,M、N、I、H分别是边BC、AD上的三等分点,E、F、G是边CD上的四等分点,图中阴影部分的面积是
如图,正方形ABCD的边长为12,P是边AB上的任意一点,M、N、I、H分别是边BC、AD上的三等分点,E、F、G是边CD上的四等分点,图中阴影部分的面积是 如图,正方形ABCD的边长等于21,它被分成四个长方形:CPFN,BMFP,AQEM,DNEQ.这四个长方形的面积之比为1:2:3:4,若图中的阴影部分是一个正方形,那么这个正方形的面积是
如图,正方形ABCD的边长等于21,它被分成四个长方形:CPFN,BMFP,AQEM,DNEQ.这四个长方形的面积之比为1:2:3:4,若图中的阴影部分是一个正方形,那么这个正方形的面积是 如图中,ABCD是边长为A的正方形,分别以AB、BC、CD、DA为直径画半圆,求这四个半圆弧所围成的阴影部分的面积.
如图中,ABCD是边长为A的正方形,分别以AB、BC、CD、DA为直径画半圆,求这四个半圆弧所围成的阴影部分的面积.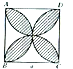 如图中,ABCD是边长为A的正方形,分别以AB、BC、CD、DA为直径画半圆,求这四个半圆弧所围成的阴影部分的面积.
如图中,ABCD是边长为A的正方形,分别以AB、BC、CD、DA为直径画半圆,求这四个半圆弧所围成的阴影部分的面积.