题目内容
 如图,E,F,G,H是边长为2的正方形ABCD各边的中点,则图中阴影部分的面积等于________.
如图,E,F,G,H是边长为2的正方形ABCD各边的中点,则图中阴影部分的面积等于________.

分析:如图,阴影部分的面积可以分成下面的两部分,中间的红色正方形,和外周绿色的四个三角形,不难看出这四个三角形的面积都是相等的,所以这里只要求出小正方形的面积和外部的一个小绿色三角形的面积即可解决问题.
(1)红色小正方形的面积可以利用大正方形的面积进行计算;
(2)要求绿色三角形的面积,只要求出△APG的面积即可,△APG的面积等于大正方形的面积-△ADG-△BCG-△ABF+△BPF,因为E,F,G,H是边长为2的正方形ABCD各边的中点:△ADG=△BCG=△ABF=
 ×1×2=1;所以只要求得△BPF的面积即可解决问题,根据已知不难得出△BPF与△ABP相似,相似比是1:2,那么它们的面积的比是1:4,所以可得:△BPF的面积是△ABF的
×1×2=1;所以只要求得△BPF的面积即可解决问题,根据已知不难得出△BPF与△ABP相似,相似比是1:2,那么它们的面积的比是1:4,所以可得:△BPF的面积是△ABF的 ,所以:△BPF=
,所以:△BPF=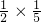 =
= ,由此即可求得小绿色三角形的面积.
,由此即可求得小绿色三角形的面积.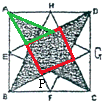
解答:
 解:(1)把中间的小正方形单独分析如右图:把所有的空白处拼起来等于4个与阴影部分相同的正方形,
解:(1)把中间的小正方形单独分析如右图:把所有的空白处拼起来等于4个与阴影部分相同的正方形,也就是说阴影部分的正方形是大正方形的
 ,
,已知大正方形的面积是2×2=4,
所以这个小正方形的面积是4×
 =
= ;
;(2)根据上图,E 是中点,ED∥BG,
可得:小绿色三角形与三角形APG相似,相似比是1:2,那么面积比是1:4,
根据题干分析可得:
△APG的面积=大正方形的面积-△ADG-△BCG-△ABF+△BPF,
=4-
 -
- -
-
 ,
,=
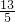 ,
,所以小绿色三角形的面积为:
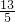 ×
× =
=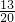 ;
;故阴影部分的面积为:

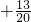 ×4=
×4= ;
;故答案为:
 .
.点评:此题是较复杂的图形的面积计算问题,这里关键是把这个不规则的图形转化成一个正方形和面积相等的四个小三角形进行分析计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,正方体的边长是10厘米,E、F、G、H分别是正方体底面各边的中点,这四点依次与正方体的顶点K连接,求阴影部分的体积(保留两位小数).
如图,正方体的边长是10厘米,E、F、G、H分别是正方体底面各边的中点,这四点依次与正方体的顶点K连接,求阴影部分的体积(保留两位小数). 如图所示,E,F,G,H分别是四边形各边中点,EG与FH交于点O,s1,s2,s3及 S4分别表示四个小四边形的面积.试比较 s1+s3与 s2+s4的大小?
如图所示,E,F,G,H分别是四边形各边中点,EG与FH交于点O,s1,s2,s3及 S4分别表示四个小四边形的面积.试比较 s1+s3与 s2+s4的大小?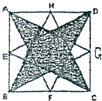 如图,E,F,G,H是边长为2的正方形ABCD各边的中点,则图中阴影部分的面积等于
如图,E,F,G,H是边长为2的正方形ABCD各边的中点,则图中阴影部分的面积等于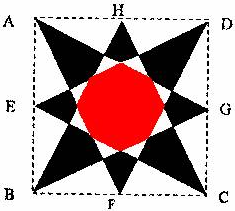 如图中,ABCD是边长为1的正方形,A,E,F,G,H分别是四条边AB,BC,CD,DA的中点,计算图中红色八边形的面积.
如图中,ABCD是边长为1的正方形,A,E,F,G,H分别是四条边AB,BC,CD,DA的中点,计算图中红色八边形的面积.