题目内容
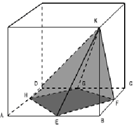如图，正方体的边长是10厘米，E、F、G、H分别是正方体底面各边的中点，这四点依次与正方体的顶点K连接，求阴影部分的体积（保留两位小数）．分析：根据题干，阴影部分的立体图形是一个高为10厘米的棱锥体，由此求得它的底面积即可解决问题．
解答：解：因为E、F、G、H分别是正方体底面各边的中点，所以四边形EFGH的面积是正方形ABCD的面积的一半，
10×10÷2=50（平方厘米），
所以这个阴影部分的体积是：
×50×10≈166.67（立方厘米），
答：阴影部分的体积大约是166.67立方厘米．
10×10÷2=50（平方厘米），
所以这个阴影部分的体积是：
| 1 |
| 3 |
答：阴影部分的体积大约是166.67立方厘米．
点评：此题考查了棱锥的体积=
×底面积×高这一公式的计算应用，关键是根据正方体的底面积求得这个棱锥的底面积．
| 1 |
| 3 |
练习册系列答案
相关题目
有一个正方体，边长是5．如果它的左上方截去一个边长分别是5、3、2的长方体（如图），求它的表面积减少的百分比是少？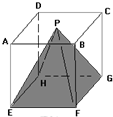
如图，一个边长是5厘米的正方体，是由125个边长为1厘米的小正方体组成的．P为上底面ABCD的对角线的交点．分别用通过P、E、F三点的平面，P、F、G三点的平面，P、H、G三点的平面，P、H、E三点的平面把正方体切开，则最后剩下的立体图形中包含
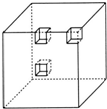如图，有一个边长为20厘米的大正方体，分别在它的角上、棱上、面上各挖掉一个大小相同的小立方体后，表面积变为2454平方厘米，挖掉的小立方体的棱长是
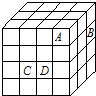48个相同的小正方体叠成（如图）的长方体，每个小正方体的边长为1厘米，在取走A，B，C，D四个小正方体后，这个几何体的表面积是