题目内容
一条直线上放着一个长方形①,它的长和宽分别是4厘米和3厘米,对角线长5厘米.让这个长方形绕依次顺时针旋转90°,最终长方形①的A点到达了H点的位置.求点A所走过的总路程.


分析:从图1到2,A点没变;从图2到图3,A点走了
个半径为3厘米的圆的周长,即
π厘米;从图3到图4,A点走过的距离就是
个半径为5厘米的圆的周长,即
π厘米;从图4到图5,A走了
个半径为4厘米的圆,即2π厘米,据此解答.
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 4 |
| 5 |
| 2 |
| 1 |
| 4 |
解答:解:2×3.14×3×
+2×3.14×5×
+2×3.14×4×
,
=(3+5+4)×2×3.14×
,
=12×3.14×
,
=6×314,
=18.84(厘米).
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
=(3+5+4)×2×3.14×
| 1 |
| 4 |
=12×3.14×
| 1 |
| 2 |
=6×314,
=18.84(厘米).
点评:此题重点是要考虑A点所走过的轨迹,除第一次外,以后每次走过的轨迹都是
圆形,根据圆的周长公式,即可解决.
| 1 |
| 4 |

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
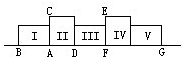 (如图)一条直线上放着一个长方形Ⅰ,它的长与宽分别等于3厘米与4厘米,对角线恰好是5厘米,让这个长方形绕一个顶点A顺时针旋转90度后到了长方形Ⅱ的位置,此时B点到了C点的位置,如此连续做四次后,A点到了G点的位置,求A点所走过的总路程的长为
(如图)一条直线上放着一个长方形Ⅰ,它的长与宽分别等于3厘米与4厘米,对角线恰好是5厘米,让这个长方形绕一个顶点A顺时针旋转90度后到了长方形Ⅱ的位置,此时B点到了C点的位置,如此连续做四次后,A点到了G点的位置,求A点所走过的总路程的长为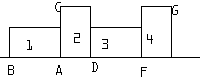 一条直线上放着一个长方形(在Ⅰ的位置),它的长与宽分别是4厘米和3厘米,对角线恰好是5厘米,让这个长方形绕一个顶点A顺时针旋转90度后,到了Ⅱ的位置,此时B点到了C的位置,如此连续做三次后,A点到了G的位置,A点所走的总路程是
一条直线上放着一个长方形(在Ⅰ的位置),它的长与宽分别是4厘米和3厘米,对角线恰好是5厘米,让这个长方形绕一个顶点A顺时针旋转90度后,到了Ⅱ的位置,此时B点到了C的位置,如此连续做三次后,A点到了G的位置,A点所走的总路程是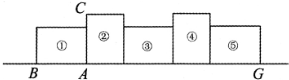
 (如图)一条直线上放着一个长方形Ⅰ,它的长与宽分别等于3厘米与4厘米,对角线恰好是5厘米,让这个长方形绕一个顶点A顺时针旋转90度后到了长方形Ⅱ的位置,此时B点到了C点的位置,如此连续做四次后,A点到了G点的位置,求A点所走过的总路程的长为________(圆周率按3计算).
(如图)一条直线上放着一个长方形Ⅰ,它的长与宽分别等于3厘米与4厘米,对角线恰好是5厘米,让这个长方形绕一个顶点A顺时针旋转90度后到了长方形Ⅱ的位置,此时B点到了C点的位置,如此连续做四次后,A点到了G点的位置,求A点所走过的总路程的长为________(圆周率按3计算).