题目内容
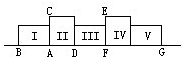 (如图)一条直线上放着一个长方形Ⅰ,它的长与宽分别等于3厘米与4厘米,对角线恰好是5厘米,让这个长方形绕一个顶点A顺时针旋转90度后到了长方形Ⅱ的位置,此时B点到了C点的位置,如此连续做四次后,A点到了G点的位置,求A点所走过的总路程的长为
(如图)一条直线上放着一个长方形Ⅰ,它的长与宽分别等于3厘米与4厘米,对角线恰好是5厘米,让这个长方形绕一个顶点A顺时针旋转90度后到了长方形Ⅱ的位置,此时B点到了C点的位置,如此连续做四次后,A点到了G点的位置,求A点所走过的总路程的长为18厘米
18厘米
(圆周率按3计算).分析:由Ⅰ到Ⅱ时A点是不动的,所以走过的路程为0;
由Ⅱ到 III,是以AD为半径走了90度,也就是
个以AD为半径圆的周长;
由III 到 IV,是以长方形的对角线为半径走了90度,也就是
个以长方形的对角线半径圆的周长;
由IV到 V,是以和EF相等长度的长方形的边为半径走了90度,也就是
个以EF相等长度的长方形的边为半径圆的周长;
最后把这四个长度加起来,就是A点到G点走过的总路程.
由Ⅱ到 III,是以AD为半径走了90度,也就是
| 1 |
| 4 |
由III 到 IV,是以长方形的对角线为半径走了90度,也就是
| 1 |
| 4 |
由IV到 V,是以和EF相等长度的长方形的边为半径走了90度,也就是
| 1 |
| 4 |
最后把这四个长度加起来,就是A点到G点走过的总路程.
解答:解:由题意和以上分析知,
由Ⅰ到ⅡA点所走过的路程 0;
由Ⅱ到 III A点所走过的路程 2π×3×
;
由III 到 IV A点所走过的路程 2π×5×
;
由IV到 V A点所走过的路程 2π×4×
;
A点到G点所走过的总路程的长:0+2π×3×
+2π×5×
+2π×4×
=6π=18 (厘米);
故答案为:18厘米.
由Ⅰ到ⅡA点所走过的路程 0;
由Ⅱ到 III A点所走过的路程 2π×3×
| 1 |
| 4 |
由III 到 IV A点所走过的路程 2π×5×
| 1 |
| 4 |
由IV到 V A点所走过的路程 2π×4×
| 1 |
| 4 |
A点到G点所走过的总路程的长:0+2π×3×
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
故答案为:18厘米.
点评:此题考查了分别以长方体的两个边和对角线为半径画圆,只不过A所画圆走过的路程不是一个完整的圆,而是
个圆的周长.
| 1 |
| 4 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
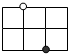 如图所示,在这个小棋盘上,将一颗白子和一颗黑子 放在棋盘线交叉点上,但不能在同一条直线上,共有
如图所示,在这个小棋盘上,将一颗白子和一颗黑子 放在棋盘线交叉点上,但不能在同一条直线上,共有 (如图)一条直线上放着一个长方形Ⅰ,它的长与宽分别等于3厘米与4厘米,对角线恰好是5厘米,让这个长方形绕一个顶点A顺时针旋转90度后到了长方形Ⅱ的位置,此时B点到了C点的位置,如此连续做四次后,A点到了G点的位置,求A点所走过的总路程的长为________(圆周率按3计算).
(如图)一条直线上放着一个长方形Ⅰ,它的长与宽分别等于3厘米与4厘米,对角线恰好是5厘米,让这个长方形绕一个顶点A顺时针旋转90度后到了长方形Ⅱ的位置,此时B点到了C点的位置,如此连续做四次后,A点到了G点的位置,求A点所走过的总路程的长为________(圆周率按3计算).