题目内容
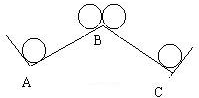 如图,一块半径为1厘米的圆板,从平面A的位置沿AB、BC滚动到位置C.如果AB=BC=10厘米,角ABC=120°.那么圆板滚过的面积是多少平方厘米?(π取3,保留小数点后面两位数字)
如图,一块半径为1厘米的圆板,从平面A的位置沿AB、BC滚动到位置C.如果AB=BC=10厘米,角ABC=120°.那么圆板滚过的面积是多少平方厘米?(π取3,保留小数点后面两位数字)分析:圆板滚过的轨迹如图,可分成这么几部分:起点与终点各剖出两个半圆,中间两段为两个长方形,在转角B处它的轨迹为半径是2厘米,圆心角是60°的扇形.据此解答.
解答:解:9×2×2+3×12+3×
×(1+1)2,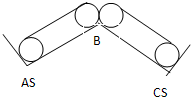
=36+3+2
=41(平方厘米);
答:圆板滚过的面积是41平方厘米.
| 60 |
| 360 |

=36+3+2
=41(平方厘米);
答:圆板滚过的面积是41平方厘米.
点评:此题考查了滚动图形的面积计算,本题需要分段进行计算,再将各段相加求解.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
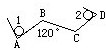 如图,一块半径为1厘米的圆板,从平面1的位置沿AB、BC、CD滚动到位置2.如果AB=BC=CD=10厘米,那么圆板滚过的面积是多少平方厘米?(π取3,保留小数点后面2位数字)
如图,一块半径为1厘米的圆板,从平面1的位置沿AB、BC、CD滚动到位置2.如果AB=BC=CD=10厘米,那么圆板滚过的面积是多少平方厘米?(π取3,保留小数点后面2位数字) (2009?河西区)如图,一个半径为1厘米的小圆盘沿着一个半径为4厘米的大圆盘外侧做无滑动的滚动.当小圆盘的中心围绕大圆盘中心转动90度后,小圆盘运动过程中扫过的面积是多少平方厘米?
(2009?河西区)如图,一个半径为1厘米的小圆盘沿着一个半径为4厘米的大圆盘外侧做无滑动的滚动.当小圆盘的中心围绕大圆盘中心转动90度后,小圆盘运动过程中扫过的面积是多少平方厘米? 如图,一个半径为1厘米的圆沿着一个直角三角形的三边滚动一周,那么这个圆的圆心所经过的总路程为
如图,一个半径为1厘米的圆沿着一个直角三角形的三边滚动一周,那么这个圆的圆心所经过的总路程为 如图,一个半径为1厘米的小圆盘沿着一个半径为4厘米的大圆盘外侧做无滑动的滚动.当小圆盘的中心围绕大圆盘中心转动90度后,小圆盘运动过程中扫过的面积是多少平方厘米?
如图,一个半径为1厘米的小圆盘沿着一个半径为4厘米的大圆盘外侧做无滑动的滚动.当小圆盘的中心围绕大圆盘中心转动90度后,小圆盘运动过程中扫过的面积是多少平方厘米?